O campo magnético de uma onda eletromagnética se propagando no vácuo é dado por . Expresse suas respostas apenas em termos de dados do problema e constantes universais.
- Determine o vetor campo elétrico desta onda. Justifique sua resposta por meio de um esquema gráfico dos vetores pertinentes.
- Determine o vetor de Poynting desta onda.
- Determine a energia total transportada pela radiação através de uma área perpendicular à frente de onda durante um intervalo de tempo igual a 4 vezes o período da onda.
Passo 1
a) Vamos resumir as características mais importantes de uma onda eletromagnética:
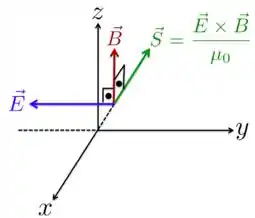
- É composta por campos elétrico e magnético que oscilam no tempo e são perpendiculares entre si;
- e são perpendiculares também à direção de propagação da onda e a relação entre os seus módulos é ;
- A direção e sentido de propagação da onda é dado pelo vetor de Poynting: , que dá, também, a quantidade de energia por unidade área transferida pela onda eletromagnética;
No caso do problema, a onda eletromagnética está se propagando no sentido de , já que o argumento da função oscilatória de é . Ou seja, o campo magnético está na direção de , mas a função que o representa mostra que a onda está caminhando no sentido e direção de .
Passo 2
Bom, dos itens acima, o campo elétrico também deve ser perpendicular à direção propagação da onda, portanto, deve estar ao longo da direção do eixo , mas precisamos ainda encontrar qual é o sentido dele.
Antes disso, o módulo já podemos achar, já que . Por isso:
Agora, partindo do vetor de Poynting, o produto vetorial tem que resultar em um vetor que está ao longo de (), já que a onda está se propagando nessa direção. Para que isso aconteça, o campo elétrico deve estar apontando na direção e sentido de . Portanto, o vetor campo elétrico é
Passo 3
b) Uma vez que já sabemos tudo (módulo, direção e sentido) sobre os vetores e , podemos calcular o vetor de Poynting:
Como , então
Portanto, a onda está se propagando na direção e sentido de , transportando a energia que armazena.
Passo 4
c) Num intervalo de tempo , a onda eletromagnética, que se propaga na direção e sentido de , percorre uma distância . Dessa maneira, se a área que a onda atravessou é , durante o tempo , a onda transportou uma energia que é igual a energia que está dentro do elemento de volume , como é mostrado na figura abaixo.
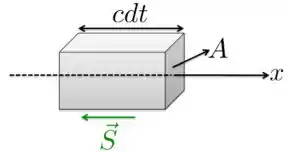
A densidade de energia , ou seja, a quantidade de energia por volume é dada por
em que é o módulo do valor médio do vetor de Poynting. Essa média é temporal, por isso, como temos uma função oscilatória ao quadrado na expressão para ,
que é independente do tempo.
Portanto, como queremos saber qual a energia total transportada pela onda num tempo de , precisamos integrar a expressão acima
O período pode ser escrito como
A energia, com isso, fica reescrita como