Questão 1: Calcule , onde é dada pela interseção das superfícies , , , , percorrida do ponto ao ponto .
Passo 1
Para resolver integrais de linha do modo direto como nos é pedido aqui nesse problema, sempre vamos seguir os três passinhos aqui:
- Parametrizar a curva
- Trocar os termos da função pelos da parametrização
- Encontrar o termo
Bora?! :D
Passo 2
Vamos então parametrizar a curva , mas por falar nisso, quem é a curva ?
Como nos pediu o exercício, a curva é esse trechinho encontrado fazendo a intercessão desse cilindro centrado em :
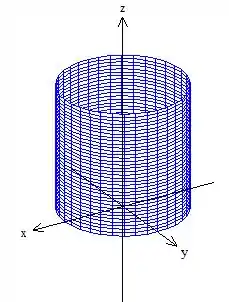
com esse outro cilindro centrado em :
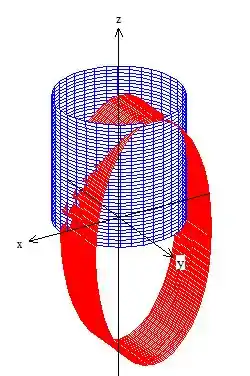
Lembre-se que estamos trabalhando com essa parte onde e , dando pra gente, essa curva aí, oh:
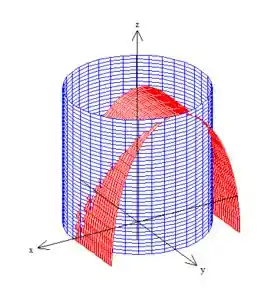
Sacou? :D
Passo 3
Como já comentamos no passo anterior, necessitamos da parametrização da curva. Bem, estamos em cima do cilindro vermelho de equação .
Para parametrizar uma curva em cima de um cilindro, basta a gente utilizar as primas das coordenadas cilíndricas:
Mas diferentemente das coordenadas cilíndricas para parametrizar uma “linha” precisamos de uma variável apenas, logo esse desaparece (Vira o raio do cilindro que a curva está sobre)
Perceba que ainda falta definirmos quem será o nessa brincadeira. Logo, venha comigo!
Passo 4
Pow, o , note no esboço da curva , que ele está na interseção dos dois cilindros
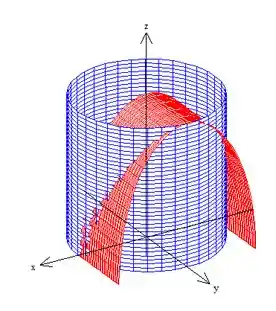
Resolver uma interseção em Matemática é resolver o sistema com as equações das superfícies envolvidas:
Isolando na primeira...
e substituindo na segunda:
extraindo a raiz...
como estamos trabalhando com a parte de cima...
Logo, a parametrização final é:
Passo 5
Lembre-se que nunca devemos sair de uma parametrização sem antes dizermos onde o parâmetro, que no caso é o , est�� variando, heim!
Essa informação, podemos tirar da informação dos pontos que curva varia:
Substituindo o primeiro ponto na curva:
Vemos que o seno tem que ser e o cosseno, , onde isso acontece? Sim! Em !
Com o ponto de chegada, encontramos o de chegada:
Novamente, cosseno, , mas o seno, ... !
Então podemos falar que o está variando de...
ou...
Passo 6
Devemos agora encontrar o termo fazendo
Calculando essa derivada da parametrização ...
Extraindo o módulo desse vetor derivada
portanto
Passo 7
Beleza! Agora devemos prosseguir substituindo na função esse , e pelos termos da parametrização:
Lembrando que ...
Passo 8
Agora basta que peguemos os três ingredientes anteriormente encontrados e substituirmos na integral...
O será substituído pela variação do parâmetro:
Agora basta que calculemos esta integral simples que apareceu!
Com uma substituição do tipo...
Não se esqueça de substituir os limites heim!
Repara que aqueles limites ficaram trocados... se mudarmos, devemos mudar o sinal da integral...