Considere a superfície S definida pela parametrização
Com
- Encontre uma equação cartesiana para a superfície S. Faça um esboço.
- Escreva o elemento de superfície dS para S e a integral usada para o cálculo da área S.
- Determine a equação do plano tangente a S no ponto definido por (2,3,0).
Passo 1
1) Observe que
Dentro de Y nós temos . Logo,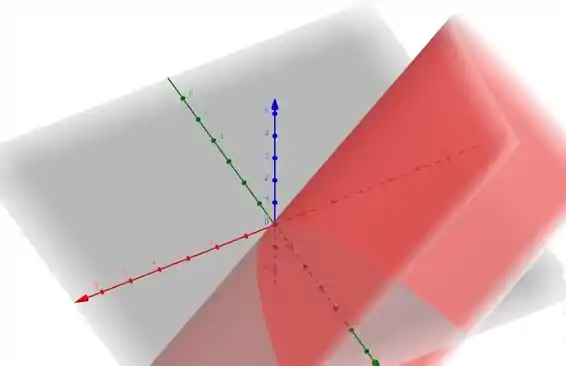 
Passo 2
Passo 3
Passo 4
2) Escreva o elemento de superfície dS para S e a integral usada para o cálculo da área S.
Vamos começar com as derivadas para caulcular a matriz do termo ds:
A derivada da parametrização em função de s fica:
A derivada em função de t fica:
Então ficamos com:
Tirando então o módulo ficamos com:
O cálculo da área será dado então por:
Passo 5
3) Determine a equação do plano tangente a S no ponto definido por (2,3,0).
Vamos ver os valores de s e t para esse ponto.
Logo,
Ficamos então com s=t=1.
O vetor normal será então:
Aplicando no ponto (1,1) ficamos com:
Com isso ficamos com o plano tangente sendo:
Resposta
Exercícios de Livros Relacionados
A base de uma cerca circular de raio 10 m é dada por x = 10 c o s t ,y = 10 s e n t . A altura da cerca na posição x , y é dada pela função h x , y = 4 + 0,01 ( x 2 - y 2 ) , portanto a altura varia 3
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais. ∫ C x y arctan z d s, onde C tem equações paramétricas x = t 2, y = t 3, z = t, 0 ≤ t ≤ π 4
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C x y e y z d y C :x = t , y = t 2 , z = t 3 , 0 ≤ t ≤ 1
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 + z 2 )d s , onde C é a interseção das superfícies x 2 16 + y 2 9 + z 2 16 = 1ey = 2 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4