Questão 3) Sabendo que um arame tem o formato da curva
Seja , a função densidade linear do arame. Determine a massa do arame.
Passo 1
Pow, é sempre bom a gente ficar atento ao vocabulário do exercício:
- Arame Curva
- Massa de Curva Uma Integral de linha
E essa integral de linha que calcula a massa é uma especial:
Veja que já temos do enunciado a função densidade , logo, temos que, antes de fazer o algebrismo, encontrar a função (Os limites de integração) e . Bora?
Passo 2
Para encontrar esses dois caras é primordial determinar antes uma parametrização para a curva (é assim com qualquer integral de linha, se lembra?). A curva é dada por...
Como você já sabe, parametrizar uma curva, de um modo geral, é colocar as três coordenadas em função de um parâmetro . Bem... Já que temos e definidos em linearmente, podemos colocar uma função do outro fácil...
Veja que podemos realizar então uma parametrização explícita, onde... é o parâmetro , o e o , sai a partir dele...
Essa basicamente já é a parametrização, mas colocando de uma forma mais charmosa...
Passo 3
Bem, eu poderia dizer que acabou a parametrização e que é só isso, mas estaria mentindo para você ! Toda parametrização nos exige dizer onde o parâmetro varia. Sim, porque a nossa curva não é infinita, certo?
Mas relaxa, que para tirar a informação de onde varia, vamos utilizar a informação do enunciado:
“ ”
Então...
Elevando ao quadrado...
Resolvendo então essa equação do segundo grau, encontramos dois valores de
Desenhando essa parábola...
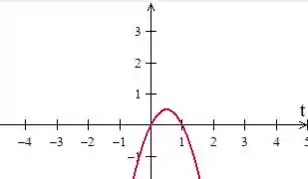
Onde percebemos que a parábola assume valores positivos entre e , ou seja, o parâmetro só pode estar entre...
Passo 4
Agora devemos encontrar , já que o intervalo de variação de já foi descoberto...
Como
Tirando o módulo...
Tirando “MMC” e colocando tudo sobre uma fração só...
Portanto o termo fica sendo...
Passo 5
Show! Agora ta acabando, basta voltar para a integral...
E substituir:
- C
- que é igual a , vira em função de ...
Resposta
Onde é unidade de massa.