Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R³

Ver Teoria
Exercício 431234567891011121314151617181920212223242526272829303132333435363738394041424445464748

Enunciado

Questão 1: Seja C a curva regular obtida pela interseção das superfícies cujas equações implícitas são z = 2 - y e z 2 = x 2 + y 2 , e tal que que z ,   y ≥ 0 .

  1. Esboce cuidadosamente as superfícies e C , destacando explicitamente os pontos de contato de C com o plano y = 0 .
  2. Determine uma parametrização regular α t para C .

    3. (Dica: Tente com uma parametrização da forma α t = t ,   y t ,   z t ,   t ∈ a ,   b . )

  3. Calcule ∫ C   f d s , para a função escalar

f x ,   y ,   z = 4 + 2 x 2 z + y 2

Passo 1

a )

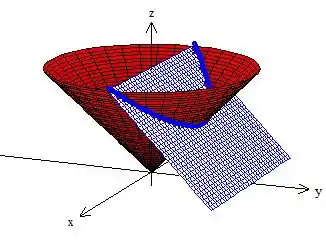
Bem, vamos começar então desenhando separadamente cada superfície que compõe a curva C , ok?

A primeira delas é a superfície plana, ou seja, o plano z = 2 - y , ele é um plano paralelo ao eixo x que passa por y = 2 quando z = 0 e passa por z = 2 quando y = 0 ...

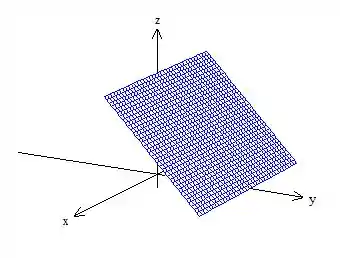
Viu só? A outra superfície é um cone mesmo: z 2 = x 2 + y 2 ...

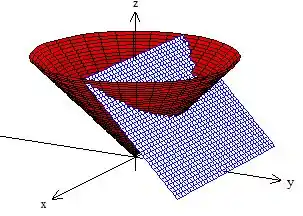
Colocando essas duas coisas jutos e observando atentamente a restrição de que z ,   y ≥ 0 , ou seja, queremos apenas a curva que está onde y é positivo e z também:

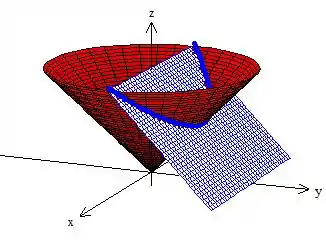
Veja ali a curva na intersecção desses dois caras =). Vou coloca-la mais evidente aqui oh:

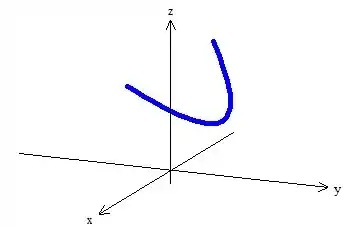
Viu só?

Passo 2

Na letra a , o problema também nos pede para destacar os pontos onde a curva encontra o plano y = 0 . Observando o nosso desenho, a gente percebe que são dois pontos, esses aqui, olha (pontos em verde):

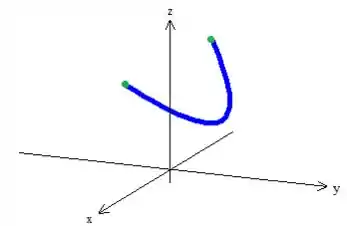
Para descobrir suas coordenadas, vejamos, sabemos que eles têm y = 0 , e estão em cima do plano, bem como do cone:

y = 0 z = 2 - y z 2 = x 2 + y 2       →             D a   s e g u n d a   e q u a ç ã o   t i r a m o s     z = 2           e     d a   t e r c e i r a … x 2 = 2 2 - 0 2     →             x = ± 2

Então esses dois pontos são:

- 2 ,   0 ,   2   e     2 ,   0 ,   2

Uma coisa que é legal destacar aqui é que esses dois pontos estão no mesmo plano y = 0 e tem a mesma altura z = 2 !

Passo 3

b )

Temos que arrumar uma parametrização para essa curva e no caso, a gente vai seguir a dica do problema e tentar arrumar uma parametrização assim:

α t = t ,   y t ,   z t ,   t ∈ a ,   b .

Veja que nesse caso, a gente está colocando x = t , ou seja, x está sendo o parâmetro (o cara independente que gera toda a curva).

Agora vejamos, o para y t , a gente sabe que a curva está em cima do cone e do plano, então, a gente pode meio que isolar o y em função de x (que é o parâmetro t )...

    z = 2 - y z 2 = x 2 + y 2       →           x 2 + y 2 = 2 - y 2       →

x 2 + y 2 = 4 - 4 y + y 2     →           - 4 y = x 2 - 4         →

y = 1 - x 2 4

Como x = t ...

y t = 1 - t 2 4

Para o z t ...

z t = 2 - y t = 1 + t 2 4

Logo, a parametrização que a gente encontrou no final das contas foi:

α t = t ,   1 - t 2 4 ,   1 + t 2 4 ,   t ∈ a ,   b .

Veja que ainda falta encontrar a variação de t (quem é esse a e b , ali). Mas calma que isso é tranquilo, pois sabemos que t = x , e vimos no passo anterior, que a curva está entre dois pontos: - 2 ,   0 ,   2   e   2 ,   0 ,   2 . Então veja que x = t deve estar entre - 2 e 2 na nossa curva !

α t = t ,   1 - t 2 4 ,   1 + t 2 4 ,   t ∈ - 2 ,   2 .

Passo 4

Assim, encontramos uma parametrização para a curva, mas será que ela é uma parametrização regular, como especificou o problema? Para verificar isso, basta lembrar que uma parametrização regular obedece:

α ' t ≠ 0 → ,         p a r a   q u a l q u e r   t ∈ - 2 ,   2

Então não tem mistérios! Basta derivar e verificar mesmo:

α ' t = 1 ,   - t 2 ,   t 2

Veja que nesse caso, independente de t , a primeira coordenada nunca é 0 , então sim!!! A a parametrização é regular !

Passo 5

c )

Agora vamos calcular a integral de linha escalar como o problema nos pediu:

∫ C   f x ,   y ,   z d s

Onde

f x ,   y ,   z = 4 + 2 x 2 z + y 2

Pow! Uma integral de linha do caso escalar, como você já sabe, sempre deve seguir esse passo a passo aqui oh:

  1. Primeiro parametrizar a curva C .
  2. Encontrar o termo d s .
  3. Trocar os termos da função pelos termos da parametrização.

Bora???

Passo 6

1 )

Bem, a ótima notícia aqui é que parametrização já está pronta do item anterior:

α t = t ,   1 - t 2 4 ,   1 + t 2 4 ,   t ∈ - 2 ,   2 .

Então vamos para...

Passo 7

2 )

Encontrar o termo d s ...

d s = α ' t d t

Com α ' t que também já foi calculado...

α ' t = 1 ,   - t 2 ,   t 2

Vamos extrair o seu módulo...

α ' t = 1 2 + - t 2 2 + t 2 2       →

α ' t = 1 + t 2 4 + t 2 4       →

α ' t = 1 + t 2 2       →

α ' t = 2 2 + t 2 2 = 2 + t 2 2

Então...

d s = 2 + t 2 2 d t

Por fim, antes de retornar a integral, temos que...

Passo 8

3 )

Trocar os termos da função pelos termos da parametrização:

f x ,   y ,   z = 4 + 2 x 2 z + y 2

Como...

α t = t ,   1 - t 2 4 ,   1 + t 2 4

Então...

f x ,   y ,   z = 4 + 2 x 2 z + y 2     →               f α t = 4 + 2 t 2 1 + t 2 4 + 1 - t 2 4 2         →

f α t = 2 2 + t 2 2 2 = 2 ⋅ 2 + t 2 4

Passo 9

Com todos esses ingredientes, podemos então retornara a integral de linha:

∫ C   f x ,   y ,   z d s = ∫ - 2 2 2 ⋅ 2 + t 2 4 ⋅ 2 + t 2 2 d t =

∫ - 2 2 2 + t 2 4 ⋅ 2 + t 2 1 d t = 1 4 ∫ - 2 2 2 + t 2 d t =

1 4 2 t + t 3 3 - 2 2 = 1 4 2 2 + 2 3 3 - 2 - 2 + - 2 3 3 =

1 4 4 + 8 3 - - 4 - 8 3 =

1 4 8 + 16 3 = 2 + 4 3 =

10 3

Resposta

a)

- 2 ,   0 ,   2   e     2 ,   0 ,   2

b) α t = t ,   1 - t 2 4 ,   1 + t 2 4 ,   t ∈ - 2 ,   2

c)

10 3

Exercícios de Livros Relacionados

A base de uma cerca circular de raio 10 m é dada por x = 10 c o s t ,y = 10 s e n t . A altura da cerca na posição x , y é dada pela função h x , y = 4 + 0,01 ( x 2 - y 2 ) , portanto a altura varia 3
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais. ∫ C x y arctan ⁡ z d s, onde C tem equações paramétricas x = t 2, y = t 3, z = t, 0 ≤ t ≤ π 4
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C x y e y z d y C :x = t , y = t 2 , z = t 3 , 0 ≤ t ≤ 1
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 + z 2 )d s , onde C é a interseção das superfícies x 2 16 + y 2 9 + z 2 16 = 1ey = 2 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4