Sejam
- Esboce a curva espacial e exiba uma parametrização regular para a mesma.
- Seja o ponto de cuja coordenada é . Encontre uma parametrização da reta tangente a em .
- Calcule as equações implícitas da reta tangente a em (i.e, para o valor do parâmetro que corresponde ao ponto ).
- Calcule a integral de linha
Passo 1
Letra a) Então, vamos começar esse problema, antes de ver a curva propriamente, entendendo quem são as superfícies que a compõe, bora?:)
Bem, a primeira delas é essa equação aqui : essa equação aí representa um paraboloide.
Mas calma, não é um paraboloide qualquer! É um paraboloide com o eixo em , pois é ele que está em função dos outros ao quadrado, percebeu?
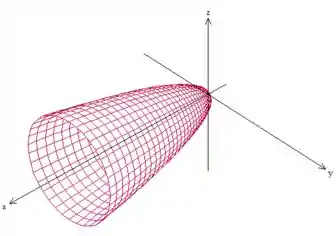
Pois bem, depois essa curva foi repartida pelo plano . Um plano paralelo ao plano , dessa forma
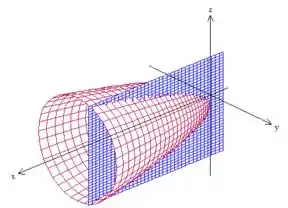
A última restrição foi que a curva estivesse :
Repare que ela já não passa mesmo abaixo de , mas acima, ela pode passar, por isso vamos pegar o pedacinho só que está indo até o
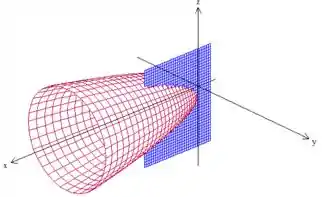
Logo a curva , nessa intercessão é

Passo 2
Ok, vamos achar então uma parametrização para essa curva que parece muito um pedaço de parábola.
Bem, como fizemos graficamente, essa curva foi a intersecção do plano com :
Epa! É realmente uma parábola no espaço
Se chamarmos ,
e lembrando que a parábola está em cima do plno , temos uma boa parametrização explícita da forma
Para descobrir o limite , olhamos para o limite que nos foi dado, ou seja, a curva não pode passar de . Como ...
Ou seja, está entre esse e :
Passo 3
Letra b) A primeira coisa que nos devemos perguntar aqui é: qual é a forma de uma reta parametrizada mesmo? ![]()
Bem, lá da álgebra vimos que se tivermos um vetor tangente e o ponto onde a gente quer, a gente consegue a reta paramétrica, pela relação:
O legal é que o ponto a gente já tem, basta substituir lembrando que
Substituindo então o ponto
Agora para o vetor tangente , vem comigo!
Passo 4
Lembra-se de que se o problema nos dá uma curva, podemos facilmente obter os vetores tangentes a ela? Basta derivar a curva, não é mesmo?
Veja só:
Derivando cada termo em relação a
Bem, como a reta é tangente à curva, o vetor tangente que queremos é o vetor no ponto de interesse !!!
Lembrando que aqui, substituindo no vetor tangente
Então, substituindo esse vetor tangente, a equação paramétrica da reta tangente é
Passo 5
Letra c) Para encontrar essa equação, basta isolar o em uma equação e substituir nas outras.
Para facilitar, vamos seguir o que o exercício falou e pegar um valor para , nesse caso o valor que ele assumiu no ponto , ou seja,
Então
Multiplicando por quatro
Podemos igualar as duas primeiras equações
Prontinho! Não tem mais nada que possamos fazer. Essas equações indicam pra gente que a reta está na intersecção desses dois planos, percebeu?
Passo 6
Letra d) Então...
para calcular essa integral de linha, vai ser easy! Por quê?
Ué, pois já temos quase tudo pronto.
Passo 7
Para calcular essa integral de linha, vamos primeiro substituir o . Como? Ora:
A gente já tem esse : , logo
Passo 8
Substituindo na integral...
Como vamos integrar em , vamos substituir pelo limite de ,
Além disso, trocar , e pelos parâmetros, que determinamos no passo 2
Fazendo uma substituição simples...
Não se esquecendo dos limites
Epa!!!! Limites iguais? Então essa integral é !:)
Resposta
Letra a)

Letra b)
Letra c)
Letra d)