Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R³

Ver Teoria
Exercício 291234567891011121314151617181920212223242526272830313233343536373839404142434445464748

Enunciado

Questão 1: Calcule a integral de linha

∫ γ   x z - 20 d s

Onde γ é o trecho da intersecção das superfícies z = x 2 + y 2 e z = 12 - 4 y , do ponto 4 ,   - 2 ,   20 ao ponto 0 ,   2 ,   4 e que está contido no semi-espaço x ≥ 0 .

Passo 1

Bem... Para resolvermos essa integral de linha escalar, podemos sempre seguir o passo a passo a baixo:

  1. Parametrizar a curva
  2. Trocar os termos da função pelos da parametrização
  3. Encontrar o termo d s

Bora?! :D

Passo 2

Sim, parametrizar a curva C , mas a pergunta mais ideal a fazer por enquanto é: quem é a C ?

Bem, como o próprio exercício já nos disse, a curva é a interseção do paraboloide   z = x 2 + y 2 com um plano z = 12 - 4 y paralelo ao eixo x ...

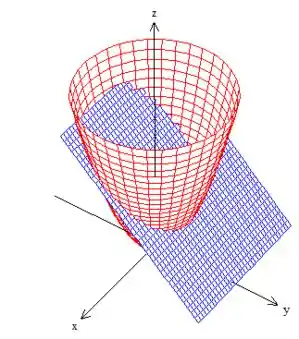
Formando, mas cuidado que só queremos a curva indo de 4 ,   - 2 ,   20 ao ponto 0 ,   2 ,   4 – lembrando ainda que essa curva está na parte onde x ≥ 0 ...

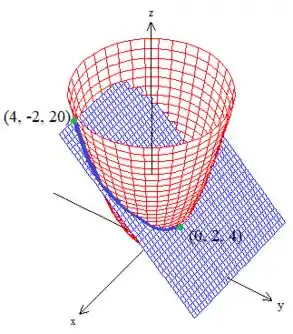
E essa curva destacada aí é a nossa queridinha γ !

Passo 3

Como já mencionamos, a curva é a intercessão de duas superfícies no espaço. Então nada mais justo que realizar essa intercessão na matemática também, concorda?

Fazer isso é resolver o sistema com as duas equações:

z = x 2 + y 2 z = 12 - 4 y         →

x 2 + y 2 = 12 - 4 y           →

x 2 + y 2 + 4 y = 12           →

Completando quadrado em y já que y + 2 2 = y 2 + 4 y + 4 ...

x 2 + y + 2 2 - 4 = 12           →

x 2 + y + 2 2 = 16

Essa equação representa uma circunferência de raio 4 e deslocada de 2 unidades e y , quer ver só?!

Passo 4

A parametrização de circunferências centradas na origem sempre será:

x = r cos ⁡ t

y = r sin ⁡ t

como a nossa curva está fora da origem e sim centrada no ponto 0 ,   - 2 , a parametrização fica

x = r cos ⁡ t

y = r sin ⁡ t - 2

Sendo r , o raio dessa curva: r = 4 ...

x = 4 cos ⁡ t

y = 4 sin ⁡ t - 2

Quanto ao z ... Bem, já vimos que ele é z = 12 - 4 y , logo

z = 12 - 4 4 sin ⁡ t - 2 =

12 - 16 sin ⁡ t + 8 =

20 - 16 sin ⁡ t

E a parametrização final fica sendo...

r → t = 4 cos ⁡ t ,   4 sin ⁡ t - 2 ,   20 - 16 sin ⁡ t

Passo 5

Você acha que a parametrização acabou ali? Se achar, calma jovem, uma parametrização só termina quando você informa onde o parâmetro, no caso t , varia na curva do enunciado, ou seja na curva γ ...

Podemos perceber na figura

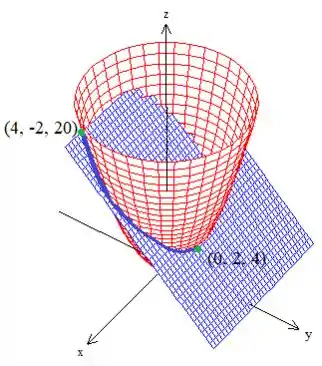
Que estamos presos na curva por dois pontos:

  • Um ponto de inicio 4 ,   - 2 ,   20 :

    • 4 ,   - 2 ,   20 = 4 cos ⁡ t ,   4 sin ⁡ t - 2 ,   20 - 16 sin ⁡ t       →

    4 = 4 cos ⁡ t         →

    cos ⁡ t = 1       →

    t = 0

  • E um ponto de fim 0 ,   2 ,   4 :

0 ,   2 ,   4 = 4 cos ⁡ t ,   4 sin ⁡ t - 2 ,   20 - 16 sin ⁡ t       →

0 = 4 cos ⁡ t         →

cos ⁡ t = 0       →

t = π 2

Veja então que bastou pegar os pontos e substituir na parametrização da curva, para descobrir o inicio e o fim do parâmetro t na curva:

0 ≤ t ≤ π 2

Passo 6

Sendo assim, a nossa próxima função aqui é justamente mudar a função f x ,   y ,   z = x z - 20 para os termos dessa parametrização (basta trocar esse x , y e z aí):

f x ,   y ,   z =   x z - 20         →

f r t = 4 cos ⁡ t 20 - 16 sin ⁡ t - 20   →

f r t = - 64 cos ⁡ t sin ⁡ t

Passo 7

Devemos agora encontrar o termo d s fazendo

d s = r ' t d t

Derivando a curva, portanto...

r t = 4 cos ⁡ t ,   4 sin ⁡ t - 2 ,   20 - 16 sin ⁡ t →       r ' t = - 4 sin ⁡ t , 4 cos ⁡ t ,   - 16 cos ⁡ t

extraindo o módulo desse vetor derivada...

r ' t = - 4 sin ⁡ t 2 + 4 cos ⁡ t 2 + - 16 cos ⁡ t 2 =

r ' t = 16   sin 2 ⁡ t + 16 cos 2 ⁡ t + 16 2 cos 2 ⁡ t =

r ' ( t ) = 16 sin 2 ⁡ t + cos 2 ⁡ t + 16 2 cos 2 ⁡ t =

r ' ( t ) = 16 + 16 2 cos 2 ⁡ t =

r ' ( t ) = 16 1 + 16 cos 2 ⁡ t =

r ' ( t ) = 4 1 + 16 cos 2 ⁡ t

portanto

d s = 4 1 + 16 cos 2 ⁡ t d t

Passo 8

Agora basta que peguemos os três ingredientes anteriormente encontrados e substituirmos na integral...

∫ γ   x z - 20 d s

O γ será substituído pela variação do parâmetro:

∫ γ   x z - 20 d s = ∫ 0 π 2 - 64 cos ⁡ t sin ⁡ t ⋅ 4 1 + 16 cos 2 ⁡ t d t =

- 256 ∫ 0 π 2 cos ⁡ t sin ⁡ t ⋅ 1 + 16 cos 2 ⁡ t d t

Agora basta que calculemos esta integral simples que apareceu fazendo uma substituição...

1 + 16 cos 2 ⁡ t = u         →               d u = - 32 cos ⁡ t sin ⁡ t d t                   o u

cos ⁡ t sin ⁡ t d t = - d u 32

Não se esquecendo de também de trocar os limites...

t = 0                       →                       u = 1 + 16 cos 2 ⁡ 0 = 17

t = π 2                       →                       u = 1 + 16 cos 2 ⁡ π 2 = 1

Logo...

- 256 ∫ 0 π 2 cos ⁡ t sin ⁡ t ⋅ 1 + 16 cos 2 ⁡ t d t = - 256 ∫ 17 1 u   - d u 32 =

256 32 ∫ 17 1 u   d u =

8 2 3 u 3 2 17 1 =

8 2 3 - 2 3 17 3 2 =

16 3 1 - 17 3 2

Resposta

16 3 1 - 17 3 2

Exercícios de Livros Relacionados

A base de uma cerca circular de raio 10 m é dada por x = 10 c o s t ,y = 10 s e n t . A altura da cerca na posição x , y é dada pela função h x , y = 4 + 0,01 ( x 2 - y 2 ) , portanto a altura varia 3
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais. ∫ C x y arctan ⁡ z d s, onde C tem equações paramétricas x = t 2, y = t 3, z = t, 0 ≤ t ≤ π 4
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C x y e y z d y C :x = t , y = t 2 , z = t 3 , 0 ≤ t ≤ 1
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 + z 2 )d s , onde C é a interseção das superfícies x 2 16 + y 2 9 + z 2 16 = 1ey = 2 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4