Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R³

Ver Teoria
Exercício 231234567891011121314151617181920212224252627282930313233343536373839404142434445464748

Enunciado

Seja C a curva regular espacial dada pela interseção das superfícies

x 2 = 1 - z 2 - y 2 ,           z ≥ - 1 2                           e                         z - x = 0 .

  1. Faça o esboço de C .
  2. Descreva uma parametrização regular de C .
  3. Calcule as equações implícitas da reta tangente a C pelo ponto - 2 2 ,   0 ,   2 2 .
  4. Calcule a integral de linha ∫ C   2 y x 3 + y 3   d s .

Passo 1

a )

Bem, para esboçar a curva C , antes temos que conhecer bem as superfícies que estão a definindo. A primeira superfície dada por essa equação bizarra

x 2 = 1 - z 2 - y 2

não é tão chata quanto parece, pois man, se você arrumar essa expressão um pouquinho...

x 2 + y 2 + z 2 = 1

Olha só como ficou mais elegante! É uma esfera de raio 1

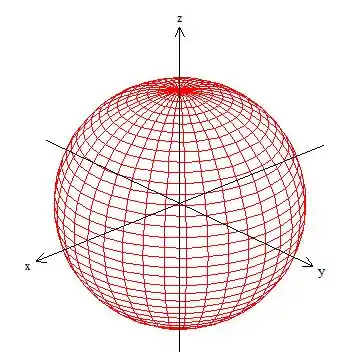
mas calma, só queremos a parte da esfera que está acima do plano z = - 1 2 ...

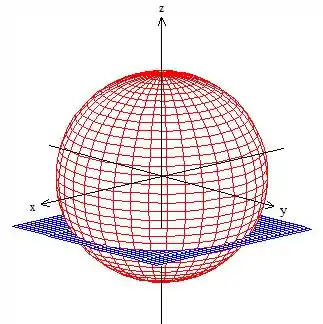
Passo 2

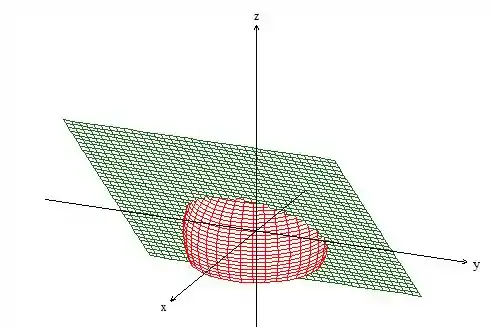
A outra superfície também não é muito feia! É um plano z = x . Se estivéssemos no plano x z , essa equação nos representaria uma reta, como estamos no espaço, temos uma coordenada a mais. Mas como a equação independe de y , é como se “puxássemos” a reta em torno de y :

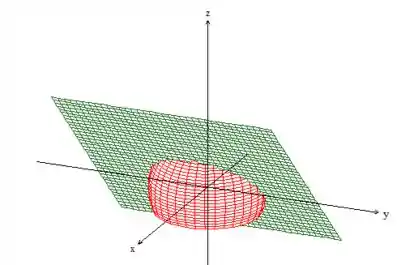
Eis a curva C na intersecção dessas coisas ;)

Passo 3

b )

Bem, a curva está definida na intersecção da esfera com o plano. Na matemática, essa intersecção é dada pelo sisteminha com as equações de ambas as superfícies...

x 2 = 1 - z 2 - y 2 z = x           ⇒             x 2 = 1 - x 2 - y 2           ⇒  

2 x 2 + y 2 = 1

Epa! Essa equação nos representa uma elipse ao redor de y , podemos parametriza-la utilizando a comparação com...

cos 2 ⁡ t + sin 2 ⁡ t = 1

2 x 2 + y 2 = 1

Por comparação...

2 x = cos ⁡ t   →           x = cos ⁡ t 2

y = sin ⁡ t

Como a curva está em cima de z = x ...

z = cos ⁡ t 2

Então, uma boa parametrização para a curva é...

γ t = cos ⁡ t 2 , sin ⁡ t ,   cos ⁡ t 2

Agora é aquilo neh... Nunca saímos de uma parametrização sem antes determinar onde varia a variável!

Passo 4

Bem, para encontra a restrição do parâmetro t , vamos usar a única restrição do nosso problema que até agora não entrou na jogada...

z ≥ - 1 2

Como z é...

cos ⁡ t 2 ≥ - 1 2           →

cos ⁡ t ≥ - 2 2

Uma boa forma de saber quem é esse t , é olhando para o ciclo trigonométrico...

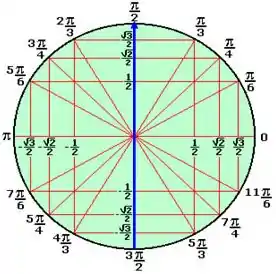
Perceba que se o ângulo estiver variando de - 135 ° até o 135 ° , o cosseno é sempre maior que esse valor. Logo...

- 3 π 4 ≤ t ≤ 3 π 4

Passo 5

Parametrização concluída, só nos resta saber se ela é regular ou não. Para isso, basta calcular a derivada da parametrização...

γ t = cos ⁡ t 2 , sin ⁡ t ,   cos ⁡ t 2       →         γ ' t = - sin ⁡ t 2 , cos ⁡ t ,   - sin ⁡ t 2

Temos que averiguar o t que...

γ ' t = - sin ⁡ t 2 , cos ⁡ t ,   - sin ⁡ t 2 = 0 ,   0 ,   0

Como o seno e o cosseno nunca se anulam no mesmo lugar, essa é uma parametrização regular ;)

Passo 6

c )

Bem, acho mais fácil primeiro encontramos, no caso de uma reta no espaço, as equações paramétricas dessa reta. Toda reta no espaço, pode ser escrita da forma...

x = a + v 1 r

y = b + v 2 r

z = c + v 3 r

Onde o ponto a ,   b ,   c é um ponto pertencente a reta, no caso, - 2 2 ,   0 ,   2 2 :

x = - 2 2 + v 1 r

y = v 2 r

z = 2 2 + v 3 r

Já o vetor v → = v 1 ,   v 2 ,   v 3 , é o vetor de direção da reta. Como a reta é tangente a curva, nesse ponto já mencionado, a derivada da curva nesse ponto me dá a direção dessa reta...

γ ' t = - sin ⁡ t 2 , cos ⁡ t ,   - sin ⁡ t 2

Agora quem t ?

Sabemos que o ponto - 2 2 ,   0 ,   2 2 é um ponto da curva...

γ t = cos ⁡ t 2 , sin ⁡ t ,   cos ⁡ t 2 = - 2 2 ,   0 ,   2 2

Como sin ⁡ t = 0 ... t ó pode ser nulo, então...

γ ' 0 = - sin ⁡ 0 2 , cos ⁡ 0 ,   - sin ⁡ 0 2 =

0 ,   1 ,   0

Esse é o vetor de direção da reta tangente v → = v 1 ,   v 2 ,   v 3 = 0 ,   1 ,   0 Substituindo na reta...

x = - 2 2

y = r

z = 2 2

Eis as equações paramétrica da reta tangente σ t no ponto pedido...

σ t = - 2 2 ,   r ,   2 2

Passo 7

d )

Agora, depois de tuuuudo isso, calculemos a integral de linha...

∫ C   2 y x 3 + y 3   d s

Normalmente seguimos um passo a passo bem maroto:

1º - Parametrizamos a curva...

2º - Encontramos o termo d s ...

3º - Em seguida buscamos a função que estamos integrando em teremos da parametrização.

Mas a nossa sorte, é que o primeiro cara já está feito, e a segunda tarefa quase toda completa. A única diferença é que...

d s = γ ' t d t

Como a derivada nós já temos, basta extrair o módulo...

γ ' t = - sin ⁡ t 2 , cos ⁡ t ,   - sin ⁡ t 2     →

γ ' t = - sin ⁡ t 2 2 + cos ⁡ t 2 + - sin ⁡ t 2 2     →

γ ' t = sin 2 ⁡ t 2 + cos 2 ⁡ t + sin 2 ⁡ t 2     →

γ ' t = 1 = 1

Logo...

d s = �� ' t d t       →           d s = d t

Passo 8

Enquanto isso, a terceira tarefa ainda não está concluída, afinal devemos substituir os termos da parametrização na função...

Como

γ t = cos ⁡ t 2 , sin ⁡ t ,   cos ⁡ t 2

A função...

2 y x 3 + y 3   =

2 sin ⁡ t cos ⁡ t 2 3 + sin ⁡ t 3 =

2 sin ⁡ t cos 3 ⁡ t 2 2 + sin 3 ⁡ t =

sin ⁡ t cos 3 ⁡ t 2 + sin 3 ⁡ t

Passo 9

Substituindo na integral de linha...

∫ C   2 y x 3 + y 3   d s = ∫ - 3 π 4 3 π 4 sin ⁡ t cos 3 ⁡ t 2 + sin 3 ⁡ t   d t =

Arrumando essas funções trigonométricas de forma a simplificar...

∫ - 3 π 4 3 π 4 sin ⁡ t cos 3 ⁡ t 2 + sin ⁡ t sin 2 ⁡ t   d t =

∫ - 3 π 4 3 π 4 sin ⁡ t cos 3 ⁡ t 2 + sin ⁡ t 1 - cos 2 ⁡ t   d t =

∫ - 3 π 4 3 π 4 sin ⁡ t cos 3 ⁡ t 2 + sin ⁡ t - sin ⁡ t cos 2 ⁡ t   d t =

∫ - 3 π 4 3 π 4 sin ⁡ t cos 3 ⁡ t 2 + 1 - cos 2 ⁡ t   d t

Fazendo uma substituição...

cos ⁡ t = a       →             d a = - sin ⁡ t d t           o u         sin ⁡ t d t = - d a

t = - 3 π 4                   →                   a = cos ⁡ - 3 π 4 = - 2 2

t = 3 π 4                   →                   a = cos ⁡ 3 π 4 = - 2 2

Como o limite foi o mesmo, nem precisa terminar a conta, pois o resultada vai ser...

∫ C   2 y x 3 + y 3   d s = 0

Resposta

a )

b )

γ t = cos ⁡ t 2 , sin ⁡ t ,   cos ⁡ t 2

- 3 π 4 ≤ t ≤ 3 π 4

c )     σ t = - 2 2 ,   r ,   2 2

d )     0

Exercícios de Livros Relacionados

A base de uma cerca circular de raio 10 m é dada por x = 10 c o s t ,y = 10 s e n t . A altura da cerca na posição x , y é dada pela função h x , y = 4 + 0,01 ( x 2 - y 2 ) , portanto a altura varia 3
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais. ∫ C x y arctan ⁡ z d s, onde C tem equações paramétricas x = t 2, y = t 3, z = t, 0 ≤ t ≤ π 4
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C x y e y z d y C :x = t , y = t 2 , z = t 3 , 0 ≤ t ≤ 1
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 + z 2 )d s , onde C é a interseção das superfícies x 2 16 + y 2 9 + z 2 16 = 1ey = 2 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4