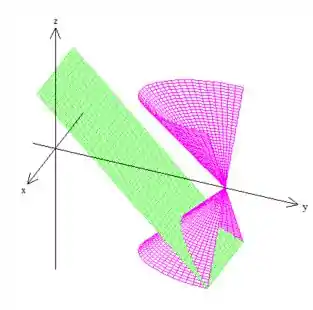
1) Considere a curva obtida como interseção da superfície com o plano , com :
- Esboce .
- Forneça uma parametrização regular de .
- Calcule a integral de linha:
- Calcule equações cartesianas da reta tangente a em .
Passo 1
Bem, para esboçar a curva , antes temos que conhecer bem as superfícies que estão a definindo. A primeira superfície dada por essa equação bizarra
não é tão chata quanto parece, pois man, se você arrumar essa expressão um pouquinho...
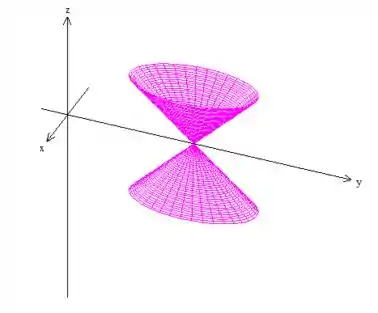
Olha só como ficou mais elegante! É um cone meio com bases elípticas, mas a única diferença notável nele, é que ele está deslocado em por unidades a direita em :
Passo 2
A outra superfície também não é muito feia! É um plano . Se estivéssemos no plano , essa equação nos representaria uma reta, como estamos no espaço, temos uma coordenada a mais. Mas como a equação independe de , é como se “puxássemos” a reta em torno de :
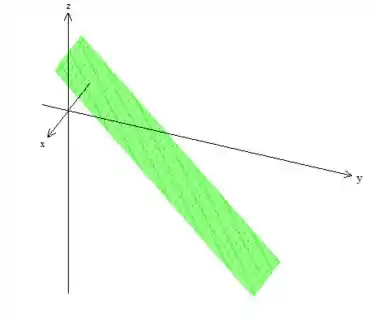
Só que esse plano está cortando o cone:
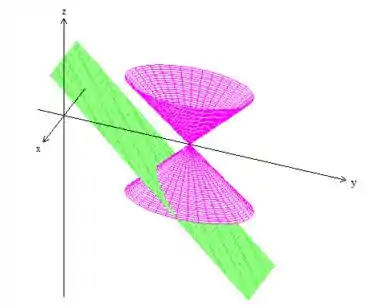
Passo 3
Agora só tem mais um detalhe: queremos a parte do corte para ser a curva , mas a parte que queremos é do .
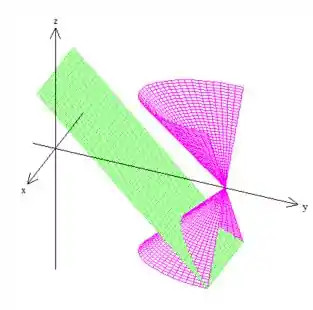
Como se do eixo central do cone para a esquerda é a curva que interessa, saca?
Eis a curva aberta pedida :D
Passo 4
Bem, a curva está definida na intersecção do cone com o plano. Na matemática, essa intersecção é dada pelo sisteminha com as equações de ambas as superfícies...
Se isolarmos o em função de na segunda e substituirmos na primeira...
Então
como ...
Epa! Se chamarmos de , temos o em função direta de ...
e quanto ao ...
Então, uma boa parametrização para a curva é...
Agora é aquilo neh... Nunca saímos de uma parametrização sem antes determinar onde varia a variável!
Passo 5
Bem, para encontra a restrição do parâmetro , vamos usar a única restrição do nosso problema que até agora não entrou na jogada...
Como é...
Então o parâmetro , varia entre e ...
Passo 6
Parametrização concluída, só nos resta saber se ela é regular ou não. Para isso, basta calcular a derivada da parametrização...
Como para nenhum valor de essa parametrização , ela é regular e portanto pode sim ser usada saca
Passo 7
Pow! Para resolver a integral de linha que é do caso escalar
Normalmente seguimos um passo a passo bem maroto:
1º - Parametrizamos a curva...
2º - Encontramos o termo ...
3º - Em seguida buscamos a função que estamos integrando em teremos da parametrização.
Mas a nossa sorte, é que o primeiro cara já está feito, e a segunda tarefa quase toda completa. A única diferença é que...
Como a derivada nós já temos, basta extrair o módulo...
Passo 8
Enquanto isso, a terceira tarefa ainda não está concluída, afinal devemos substituir os termos da parametrização na função...
Passo 9
Substituindo na integral de linha...
Dividindo essa integral em ...
Calculando a primeira integral...
Agora calculando a segunda integral fazendo uma substituição simples...
Substituindo também os limites de integração...
Então podemos fala que ...
Passo 10
Bem, acho mais fácil primeiro encontramos, no caso de uma reta no espaço, as equações paramétricas dessa reta. Toda reta no espaço, pode ser escrita da forma...
Onde o ponto é um ponto pertencente a reta, no caso,:
Já o vetor , é o vetor de direção da reta. Como a reta é tangente a curva, nesse ponto já mencionado, a derivada da curva nesse ponto me dá a direção dessa reta...
Como e no ponto mencionado, então...
Substituindo na reta...
Com o variando livremente, vemos que a reta, está amarrada a dois planos:
Essas são as equações cartesianas da reta no espaço, sempre dois planos concorrentes.
Resposta