![]()
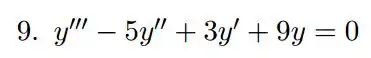
Passo 1
Precisamos resolver essa EDO
Se colocarmos na forma da equação característica
Se de cara procurarmos algumas possíveis raízes (dica: pode tentar e , inicialmente), encontramos que uma delas é:
Passo 2
A próxima coisa a fazer para encontrar as outras raízes, e diminuir o grau da nossa equação, usando o método de Briot-Ruffini. Tá lembrado?
A primeira coisa a fazer é escrever essa equação completa, colocando vezes o elevado aos graus que não aparecem, neste caso a equação já está completa.
Agora montamos o seguinte quadrinho
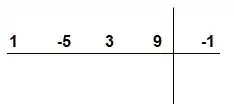
No canto superior esquerdo colocamos os coeficientes da nossa equação, no canto superior direito colocamos o valor na nossa raiz.
Agora nós fazemos os seguintes passos. Primeiro descemos o primeiro coeficiente, que vai ficar
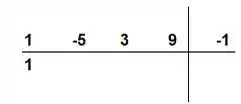
O próximo passo é multiplicar esse número que baixamos pelo número ali no canto superior direito, e depois somar com o próximo coeficiente.
Nesse caso fazemos
Esse primeiro é o coeficiente, o é nossa raiz ali no canto esquerdo, e aquele é o próximo coeficiente.
Vamos achar , colocamos esse valor embaixo do coeficiente , ficando

Deu para dar uma lembrada de Briot-Rufini né? Repetindo isso até terminar o método, vamos ficar com
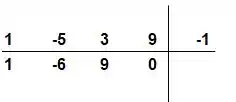
Então nossa equação reduzida fica
Passo 3
Entrando as raízes dessa nova equação
Ficamos com uma raiz dupla
Passo 4
Por fim, precisamos encontrar a solução relacionada a cada uma das raízes que determinamos.
Atenção! Viu que temos uma raiz dupla. Não esquece que precisamos considerar isso na solução e multiplicar um dos termos por . Vamos ficar com
Então a solução geral será: