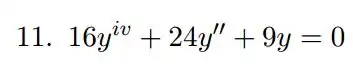
Passo 1
Preparado para resolver mais uma EDO homogênea?
Colocando na forma da equação característica
Essa é uma equação biquadrada, que podemos resolver substituindo . Fazendo essa substituição ficamos com
Resolvendo
Desfazendo a substituição
Passo 2
Perceba que nesse caso temos raízes duplas então temos que lembrar de multiplicar as soluções por , como vimos lá na teoria.
Se as raízes fossem únicas teríamos
Mas como são duplas precisamos adicionar
Então a solução geral do problema fica
Resposta
Exercícios de Livros Relacionados
20. y^((4)) - 8 y^' = 0
21. y^((8)) + 8 y^((4)) + 16 y = 0
Em cada um dos problemas de 29 a 36, encontre a solução do problema de valor inicial dado e faça seu gráfico. Como a solução se comporta quando t → ∞ ?29. y ' ' ' + y ' = 0 ;y 0 = 0 , y ' 0 = 1 ,y ' '
Nos problemas 1-36, encontre a solução geral para a equação diferencial dada. y ' ' ' + y ' ' - 2 y = 0
3. Achar a solução geral das seguintes equações diferenciais:a) f ' = 0 ; b) f n = 0 c) f ' = f d) f ' = a fa∈ R .