Uma sirene para alerta de desastres possui frequência de e com uma potência de é acionada em situações de risco. Durante um teste realizado, uma pessoa dentro de um veículo inicialmente parado a metros da sirene, não sabia que se tratava apenas de um teste. Quando ouviu a sirene, passou a se afastar em linha reta, em direção radial a sirene e com velocidade constante de . A velocidade do som é de .
a) Quanto tempo levou para a onda sonora chegar à pessoa a partir do instante em que a sirene foi acionada?
b) Determine a intensidade da onda emitida pela sirene na posição em que a pessoa se encontrava inicialmente parada.
c) Quando a pessoa começou a se afastar com velocidade constante, qual a frequência com que ela passou a ouvir a sirene?
d) Suponha agora que ao invés de uma, o alerta é composto de duas sirenes, colocadas a uma distância entre elas e que quando acionadas, geram ondas em fase e de mesma amplitude.
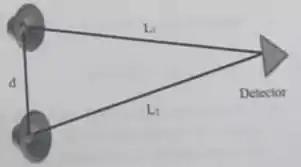
Suponha que um detector está a uma distância da sirene 1 e da sirene 2, conforme a figura. Determine qual deve ser a diferença da distância e em função da frequência e da velocidade do som para que tenhamos: (i) interferência construtiva; (ii) interferência destrutiva.
Passo 1
Fala galerinha, partiu resolver esse problema sobre ondas sonoras?
O item (a) é bem tranquilo pessoal. Ele quer saber quanto tempo demora para a onda sonora percorrer até chegar na pessoa:
Usando e (velocidade do som), achamos
Passo 2
No item (b) queremos saber qual a intensidade da onda sonora a uma distância da fonte (sirene). Para isso, temos que lembrar que a intensidade é a potência por unidade de área:
Como o som é uma onda esférica, a área em questão é área de uma esfera de raio , dada por . Assim,
Logo,
Passo 3
No item (c) vamos usar o efeito Doppler! Como o observador está se movendo e a fonte está parada, devemos usar a expressão:
Caso a fonte também tivesse em movimento, apareceria um outro fator no denominador. Lembre-se que o sinal superior corresponde ao caso de o observador estar se aproximando da fonte, enquanto o sinal inferior corresponde a situação desse problema: o observador está se afastando da fonte!
Com isso,
Usando , e , temos que
Logo,
Portanto,
Passo 4
Para terminar o problema, vamos ao item (d). O assunto agora é interferência. A diferença de caminho entre as duas ondas é
Repare que usei o módulo pois não sabemos qual caminho é o maior e qual é o menor. Para que interferência seja construtiva, a diferença de caminho deve ser um múltiplo inteiro do comprimento de onda:
Já para que a interferência seja destrutiva, deve ser um múltiplo ímpar de :
Usando que , temos que
E com isso nós finalizamos o problema 😉.