Uma ambulância emite um som com frequência f e se move com velocidade A se afastando de uma pessoa que está parada na calçada. O vento está soprando a uma velocidade V em relação ao chão, no sentido contrário ao da ambulância.
Denotando por S a velocidade do som em relação ao ar, qual é a frequência escutada pela pessoa?
Passo 1
Frequência se alterando por causa de movimentos: Efeito Doppler!
Onde O é o observador e F é a fonte sonora e é a velocidade do som naquele local.
Ah, mas tem um monte de sinal aí, como que eu escolho entre ?
Você cria um referencial que vai do OBSERVADOR PARA FONTE, se a velocidade estiver no sentido desse referencial, use +, se estiver contrária, use -.
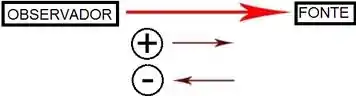
Passo 2
Vamos aplicar nosso referencial então!
A ambulância emite o som, então ela é a fonte, e a pessoa está ouvindo o som, ela é o observador.
Nosso referencial é .
A pessoa está parada, então .
A ambulância se afasta da pessoa, então ela vai no mesmo sentido do referencial, então vamos usar
Mas qual que é a velocidade do som naquele local?
Passo 3
A velocidade do som vai ser afetada pelo vento. O vento vai fazer com que o som chegue mais rápido ou mais devagar ao observador.
Como temos um vento que vai no sentido contrário da ambulância, ou seja o vento vai em direção ao observador, no mesmo sentido em que o som está se propagando.
Então o som vai acabar chegando mais rápido, por isso
Resposta
h)