Dois alto-falantes estão voltados diretamente um de frente para o outro, a uma distância . Eles emitem, em fase, um mesmo tom de A velocidade do som no local é de . Se uma pessoa caminha na direção de um alto-falante até o outro a uma velocidade de , o que ela escutará?
A) Um tom de 170Hz com volume constante
B) Um tom de 168 Hz e outro tom de 172Hz, ambos com volume constante.
C) Um tom de 170Hz cujo volume varia periodicamente, com um máximo 1 vez por segundo.
D) Um tom de 170Hz cujo volume varia periodicamente, com um máximo 2 vezes por segundo.
E) Um tom de 170Hz cujo volume varia periodicamente, com um máximo 4 vezes por segundo.
Passo 1
Aqui temos duas coisas acontecendo!
A primeira é que as frequências dos autofalantes ouvidas pela pessoa não serão . Isso porque temos o efeito Doppler!
A segunda é que temos a interferência das duas ondas!
Então vamos olhar primeiro efeito Doppler
A frequência do alto-falante da esquerda vai ser modificada por
A frequência do alto-falante da direita vai ser modificada por
Mas calma que a questão não acabou!!!! Ainda tem que fazer a interferência entre as duas ondas!!!
Passo 2
Agora temos que somar as duas ondas!
As equações das ondas são dadas por
(A diferença de sinal na frente do é por que uma onda está indo para a esquerda e a outra para direita)
A onda resultante será a soma das duas
Usando a propriedade
Ou seja, temos um efeito de batimento!
Substituindo os valores das frequências (lembrando que )
Ou seja, temos uma função cosseno que varia rapidamente sendo modulada por uma que varia lentamente.
Pela análise dessa função a parte que varia lentamente tem uma frequência de , ou seja, vemos máximos com uma frequência de .
Mas como temos uma parte rapidamente oscilando temos que mínimos acabam virando máximos também! Assim a nossa frequência para máximos de amplitude vira !
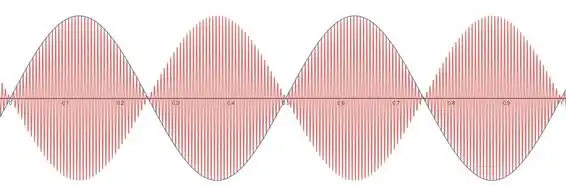
Já a parte rapidamente oscilante tem um frequência de , ou seja, temos um som com frequência de cujos máximos de intensidade ocorrem com uma frequência de !
Resposta
(E)