Um alto-falante de massa m está preso a uma mola executando um movimento oscilatório enquanto emite uma onda sonora de frequência f0 que se propaga com velocidade v0 em direção a um ouvinte parado, como ilustrado na Figura 1. A Figura 2 mostra o deslocamento da mola em função do tempo. Faça o que é solicitado abaixo e deixe suas respostas apenas em termos dos parâmetros fornecidos no texto e nas figuras (m, f0, v0, a, b).
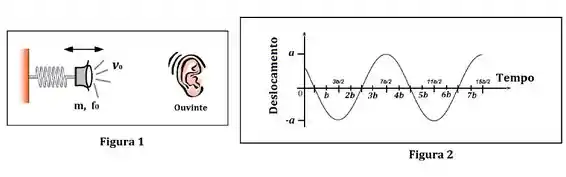
a) Encontre a menor frequência percebida pelo ouvinte.
b) Encontre a energia potencial elástica do sistema massa-mola em função do tempo.
Passo 1
a) Opa! Essa questão aí tem efeito Doppler! Vamos lembrar da fórmula da frequência:
Para um observador parado, .
Para fonte se aproximando do observador, usamos sinal negativo. Se distanciando do observador, sinal positivo.
A menor frequência percebida pelo observador vai ser então da fonte se distanciando. (Sinal positivo, denominador maior, fica menor.) Então:
E vai ser mínimo na máxima velocidade da fonte! Vamos achar essa velocidade máxima.
Passo 2
Vamos lembrar da solução do MHS:
E a velocidade, que é a derivada da posição:
Então a velocidade máxima é:
E nós já conhecemos, que é, pelo gráfico:
Nós conseguimos achar , por causa da fórmula:
E T, do gráfico é:
Então:
Passo 3
A frequência mínima percebida pelo observador vai ser então:
Em que a frequência da fonte , a velocidade do som é e a velocidade da fonte .
Passo 4
b) A energia potencial elástica é:
Não sabemos o valor de k, mas podemos descobrir. Assim:
Substituindo :
Então:
Falta achar x!
Passo 5
Vamos substituir o que já temos:
Falta achar ! Presta atenção no que eu vou fazer aqui.
Lá do gráfico, conseguimos ver que:
Então vamos substituir:
Como:
Ufa! Então agora temos x(t):
E vamos substituir na fórmula da energia:
Resposta
a)
b)