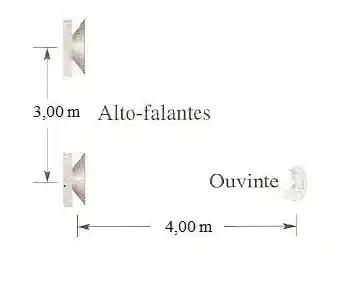
Na figura abaixo dois alto-falantes, separados por uma distância de emitem ondas sonoras em fase. Suponha que as amplitudes do som vindo dos alto-falante são aproximadamente as mesmas na posição de um ouvinte, que está a em linha reta em frente de um dos alto-falantes.

1. Para que frequências na faixa de a o ouvinte escutará um sinal máximo?
2. Para que frequências nesta faixa ele escutará um sinal mínimo?
3. Suponha agora que o alto-falante mais distante do ouvinte seja desligado e que o ouvinte comece a andar em direção ao outro alto-falante com velocidade . Se o alto-falante esta emitindo ondas com frequência , que frequência escutará o ouvinte?

Dado:

a):

Bom galera, nessa questão nós vamos analisar como a diferença dos percursos que as duas ondas sonoras tomam, influencia na frequência da onda resultante.

Bora então:

Bem, a onda sonora do alto-falante de cima vai percorrer quantos metros até atingir o ouvinte?

A resposta é simples: Como a onda se propaga em linha reta, ela vai percorrer a hipotenusa do triângulo retângulo do figura. Então:

E a outra onda vai por baixo, logo:

Então a diferença de percurso é:

Agora nós vamos usar a fórmula da interferência que vimos na teoria:

Onde é diferença de fase das duas ondas.

Bom, se a diferença de fase é múltiplo de , ocorre uma interferência construtiva e a frequência é máxima na onda resultante (:.

Vamos analisar essa situação:

Logo:

Show!

Bem, mas o que a gente quer saber são as frequências que cabem em uma determinada faixa, né?

Então vamos substituir a frequência nessa bagaça:

Sendo

Ok!Quase tudo pronto! Agora precisamos saber os valores de que estão entre e :

Para

Na faixa!

Na faixa!

Na faixa!

Pra valores maiores de a frequência ultrapassa .

Então as frequências que estão entre e para as quais o ouvinte escutará um sinal de máximo são: e