Dois alto-falantes são colocados nas posições indicadas na figura ao lado e emitem, em fase, sinais com mesma frequência. Considere que, separadamente, a amplitude de cada onda ao ponto seja .
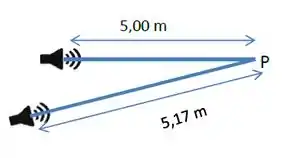
a) Para a frequência de , calcule o comprimento de onda e a diferença de fase, em termos de , entre as ondas que chegam ao ponto .
b) Determine, em função de, a amplitude da onda resultante detectada no ponto .
PARTE II
Agora os alto-falantes são colocados conforme a figura, a distância de 60,0 cm da origem do eixo x, emitindo em fase sons na frequência de .
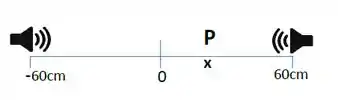
c) Encontre as posições, , do ponto , entre as fontes, onde a diferença de fase entre as ondas seja nula ou um múltiplo de (máximos de intensidade sonora).
d) Considere agora apenas o alto-falante da direita ligado. No ponto é colocado um medidor de frequências que pode se movimentar ao longo do eixo. Observa-se que o medidor detecta uma frequência de . Determine sua velocidade e o sentido do movimento.
Passo 1
a) O comprimento de onda é definido como
Logo
A diferença de fase pode ser calculada da seguinte forma
Resolvendo a equação chegamos a
Passo 2
b) A amplitude da onda resultante é a soma da amplitude emitida pelo som 1 e o som 2, logo
Então a amplitude resultante será
Passo 3
c)
As variações de comprimento serão do tipo
Para determinarmos as posições onde a diferença de fase entre as ondas seja nula ou um múltiplo de , temos q saber o comprimento de onda, para isso
Como são múltiplos de
Logo as posições serão
Passo 4
d) A frequência é definida como
o detector se afasta da fonte, se movendo para a esquerda, produzindo assim a redução da frequência detectada.
Resposta
a)
b)
c)
d)