Um apito de se move em uma circunferência com de raio com uma velocidade angular de . Quais são as frequências (a) mais baixa e (b) mais alta escutadas por um ouvinte distante, em repouso em relação ao centro da circunferência?
Passo 1
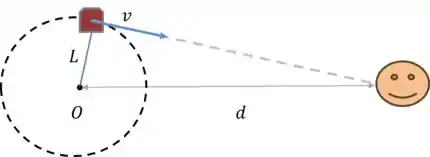
A primeira coisa aqui é a gente fazer um desenho dessa situação:
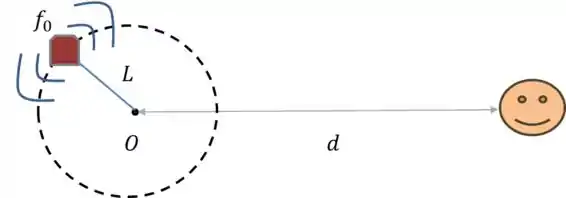
No movimento circular, a velocidade nem sempre vai estar na mesma direção da reta entre o observador e a sirene, certo? Nesses casos, como a gente viu lá na teoria, o que a gente tem que fazer é decompor a velocidade na direção da reta.
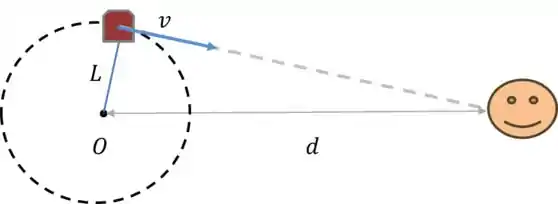
Mas calma! Como nos foi pedido as frequências extremas, não precisamos pensar nesses casos. Vamos só considerar os casos em que a velocidade tem a direção da reta que liga a sirene ao observador.
Passo 2
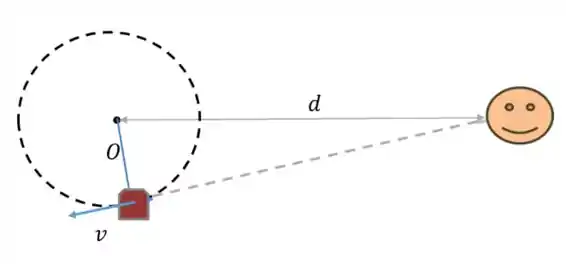
- Vamos ter a frequência mínima quando o apito estiver se afastando da fonte:
- Já para a frequência máxima, o apito estará se aproximando:
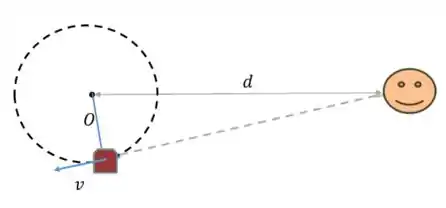
Sabemos também que:
Como a frequência do apito é e a velocidade do som é :
Passo 3
Os valores da frequência e da velocidade do som são os mesmos: