Um jato com velocidade realiza um “fly-by”(voo rasante) próximo à torre de controle de um porta-aviões, a uma altura do convés em um dia sem vento. O porta-aviões se move a uma velocidade a uma velocidade na mesma direção do avião.

Medições feitas pelo fabricante do jato indicam que a frequência do som das turbinas do jato é de com intensidade sonora de medida a 1 metro de distância. Considere a velocidade do som no ar em repouso como sendo .

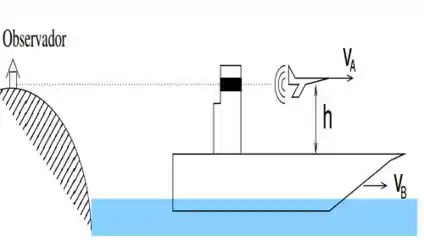
1. O avião se afasta de um observador em terra situado a mesma distância à mesma altura do avião ( Veja a figura).Durante o “fly-by”, esse observador mede uma frequência de para o som dos jatos do motor. Calcule a velocidade do jato durante o “fly-by”.
2. Determine a frequência medida por um observador dentro da torre de controle.
3. Calcule a intensidade sonora do ruído das turbinas do avião medida no convés (despreze efeitos de interferência).
4. Calcule a altura mínima para que o avião possa fazer o “fly-by” sem que a intensidade sonora no convés atinja o limiar da dor(.

b):

Nessa caso, tanto o observador quanto a fonte estão em movimento. Logo, a equação da frequência observada será:

c):

Aqui a gente precisa lembrar primeiro, a expressão pra intensidade sonora:

Onde é a potência e a área. No caso de uma onda sonora, que assume uma geometria esférica no ar, a área ali vai ser substituída pela área de uma esfera, ou seja:

Onde vai ser a distância do observador até a fonte.

Logo, sendo a intensidade a 1 m de distância do avião e a potência a uma distância

Então a intensidade em decibéis pra um convés que está a uma distância da fonte será:

Sendo 10 (dados do enunciado) e e

d):

Vamos resolver essa aqui bem mais rápido seguindo os passos do item c.No item c, chegamos nessa expressão:

Basta agora a gente fazer e igualar o valor da equação acima à :