Navios de viagens de recreio A e B movimentam-se um em direção ao outro, ambos viajando a velocidades de em relação ao sistema de referência fixo à Terra. O vento está soprando a uma velocidade de na mesma direção e sentido do movimento do barco A, como visto do referencial fixo à Terra. Há uma banda em cada navio. O oboísta do navio A toca a nota musical correspondente à frequência de 410 Hz. Os músicos do navio B ouvem esta nota e depois a executam novamente. Que frequência ouve o maestro no navio A? Considere a velocidade do som no ar como .

a) 545 Hz

b) 477 Hz

c) 440 Hz

d) 1000 Hz

e) 461 Hz

Oii pessoal, tudo bem?

Vamos lá, essa é uma clássica questão de Efeito Doppler 😊

A gente tem esse esquema aqui olha:

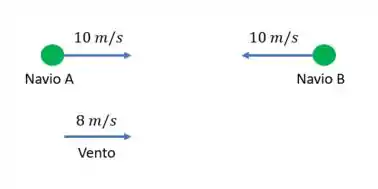
E aí um cara do navio A toca a nota musical com frequência de . Quando os músicos do navio B ouvem, eles executam essa mesma nota novamente.

Com isso, queremos saber a frequência que o maestro do navio A vai ouvir, fechou?

O passo a passo é o seguinte:

- Primeiro vamos encontrar qual a frequência que os músicos do navio B ouvem, porque é essa frequência que eles vão repetir

- A partir da frequência que eles repetem, vamos encontrar qual a frequência que a galera do navio A vai ouvir, fechou?

A fórmula de efeito Doppler quando temos influência da velocidade do vento vai ser

Onde é a frequência do observador (a famosa que queremos descobrir)

é a frequência da fonte

é a velocidade do som:

vale

é a velocidade do observador:

é a velocidade da fonte do som:

Quando o oboísta toca a frequência de , o som vem do barco A e vai no mesmo sentido do vento, então vamos usar

E como os dois barcos estão se aproximando, o sinal será de soma em cima e de subtração embaixo, fechou? Bora!