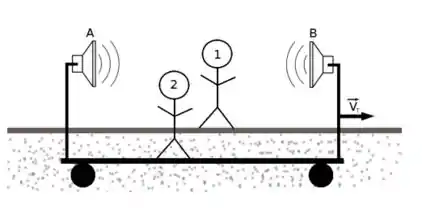
Um trem com velocidade constante dada por passa por uma plataforma. A pessoa 1 está parada na plataforma e a pessoa 2 está parada no vagão do trem. Os altos-falantes e estão acoplados no vagão do trem e quando estão ligados emitem som com a mesma frequência dada por Esta configuração pode ser observada na figura abaixo. Considere a velocidade do som sendo .
Se o alto-falante estiver ligado e o alto-falante estiver desligado, qual será a frequência do som observado pela pessoa 1 e pela pessoa 2, respectivamente?
- e .
- e .
- e
- e
- e
Passo 1
Nessa situação, é fácil calcular a frequência observada por cada observador pois corresponde a um caso simples do efeito de Doppler.
Vamos primeiro pensar no observador que está dentro do vagão. Como não há movimento relativo entre a fonte e o observador ali, a gente nem precisa aplicar a lei de Doppler (:.
Então a frequência pro observador 2 vale:
Passo 2
Agora vamos usar o efeito Doppler para calcular a frequência observada pelo observador 1. Como a fonte está se aproximando do observador, a gente vai usar o na equação abaixo:
Sendo e
Resposta
b)