UTFPR - Sem Campus - Física 1 - Provas - Teste 9 -AV2 - 2022.2 - Questão 1 - Alternativa c
Um bloco de escorrega para baixo, a partir do repouso, em um plano inclinado que faz um ângulo de com a horizontal. O coeficiente de atrito cinético é de .
Neste mesmo instante, quanto vale a energia cinética do bloco?
Passo 1
Oiie, tudo bem?
Temos aqui um problema de mecânica bastante clássico, um bloco de massa , escorregando a partir do repouso em um plano inclinado em , que nem o desenho abaixo
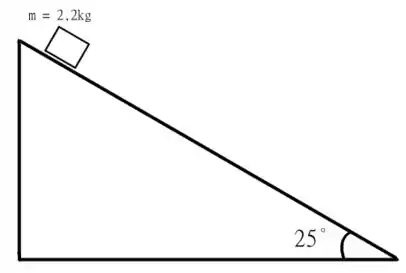
A superfície deste plano inclinado tem um coeficiente de atrito cinético . Nas alternativas anteriores construímos o diagrama de força e calculamos a variação da energia térmica para um deslocamento de como
Esta alternativa pede com que calculemos a variação da energia cinética! E, esta informação acima será necessária! Aqui vamos ter que fazer algumas considerações, primeiro faremos a conta considerando a conservação da energia e depois ver a diferença causada pela força de atrito! A conservação de energia pura nos diz que
então para começar vamos lembrar como calcular a variação da energia potencial! Belezinha? Vem comigo!
Passo 2
Novamente deixo aqui o diagrama de forças pois ele nos será útil
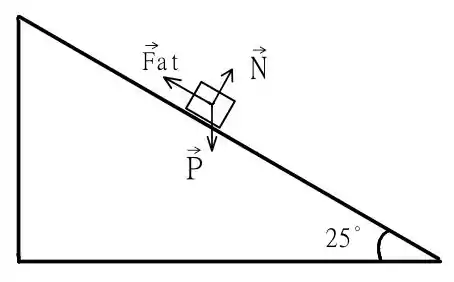
assim como o seguinte esquema dos componentes da força peso
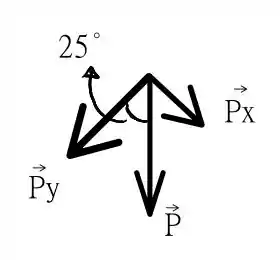
Se nos lembrarmos, temos que a energia potencial gravitacional nas proximidades da superfície da Terra pode ser aproximada com a seguinte definição
em que é a altura em que o bloco se encontra. Vamos considerar a altura na qual o bloco começa o movimento, e após o deslocamento de dois metros, de forma que temos que a variação da energia potencial é
Agora só precisamos calcular estas alturas, belezinha? Bora lá!
Passo 3
A primeira coisa que podemos fazer, é escolher um referencial em que , isso é possível pois a energia potencial é calculada em termos de uma escolha de referencial. Mas é claro que nesta escolha, precisamos calcular um adequado, nesta escolha podemos montar o seguinte triângulo retângulo para esta altura
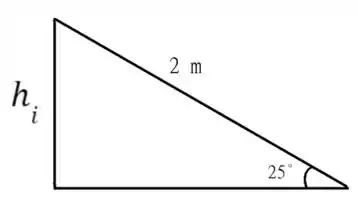
Note que para este triângulo temos
Isolando nossa altura, temos que
Portanto, a variação da energia potencial é
Okay, mas… Isso só é igual ao negativo da variação na energia cinética no caso sem força de atrito, para o nosso caso temos que considerar a energia liberada termicamente pela força de atrito! Vamos fazer isso!
Passo 4
Para o caso conservativo, temos que
Mas, como a força de atrito libera parte desta energia na forma de calor, temos que a variação da energia interna real é tal que
Ou seja, temos que a variação da energia cinética é dada por
Essa alternativa é isso! Te vejo na próxima! Tchauzinho!