Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética

Ver Teoria
Exercício 461234567891011121314151617181920212223242526272829303132333435363738394041424344454748495051525354555657585960616263

Enunciado

USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 26d

Um disco uniforme de 100   k g e raio 0,60   m está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes F 1 → = ( 60   N ) i → e F → 2 = - ( 40   N )   i → durante 5   s .

( d ) calcule a energia cinética do cilindro quando t =   5   s .

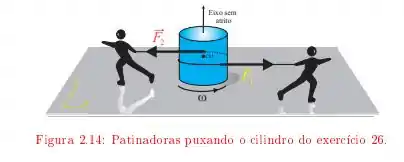
Passo 1

Oiie, tudo bem?

Temos aqui um disco uniforme que é puxado por duas patinadoras como no esquema a seguir

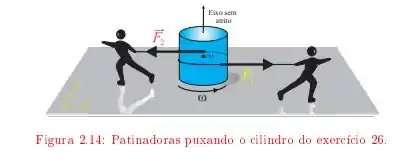
este disco tem uma massa m = 100   k g e raio r = 0,60   m . Elas aplicam forças F 1 → = ( 60   N )   i → e F → 2 = - ( 40   N )   i → de forma que o giro do disco é acelerado por ambas as forças durante 5   s , o objetivo desta alternativa é

( d ) calcule a energia cinética do cilindro quando t =   5   s .

Nas últimas alternativas obtivemos que

ω → ( t ) = ( 3,33   r a d   s - 2 )   t

Nós iremos precisar desta relação para encontrar a nossa energia cinética de rotação, uma vez que

E c r = 1 2 I ω 2

mas, a energia cinética total leva também em consideração a velocidade linear que obtivemos anteriormente como

v → ( t ) = ( 0,2   m   s - 1 )   t   i ^

já que

E c = 1 2 m v 2

Vamos fazer as contas! Bora lá!

Passo 2

Após t = 5   s a velocidade linear é

v → ( t ) = ( 0,2   m   s - 2 )   ( 5   s )   i ^ =   1   m   s - 1   i ^

a velocidade angular é

ω → ( t ) = 16,6   r a d   s - 1   k ^

em alternativas anteriores obtivemos que o momentum de inércia é

I = 18   k g   m 2

Portanto, temos que a energia cinética de rotação é tal que

E c r = 1 2 ( 18   k g   m 2 ) ( 16,6   r a d   s - 1 ) 2 = 2480   J

e, a energia cinética linear é

E c = 1 2 ( 100   k g ) ( 1   m   s - 1 ) 2 = 50   J

Portanto, a energia cinética total é dada por

E T = 2530   J

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

E T = 2530   J

Exercícios de Livros Relacionados

Em 10 de agosto de 1972, um grande meteorito atravessou a atmosfera sobre o oeste dos Estados Unidos e Canadá como uma pedra que ricocheteira na água. A bola de fogo resultante foi tão forte que pôde
10.4. Se a velocidade de uma partícula aumentar por um fator de 3, por que fator irá variar sua energia cinética?
03. Quanto vale a velocidade de um carro pequeno de 1.000k g que possui a mesma energia cinética de um caminhão de 20.000k g que trafega a 25k m / h ?
01. Qual objeto possui maior energia cinética: uma bala de 10g disparada a 500m / s ou um estudante de 75k g correndo a 5,5m / s ?
7. A massa de um átomo de oxigênio é quatro vezes maior do que a de um átomo de hélio. Em uma experiência, um átomo de hélio e outro, de oxigênio, possuem a mesma energia cinética. Qual é a razão v H