Um bloco é lançado verticalmente para cima com uma velocidade inicial , atinge uma altura máxima e retorna ao ponto do lançamento, percorrendo uma distância total de .
a) Desprezando qualquer interação dissipativa entre o ar e o bloco, calcule em termos de e a aceleração da gravidade ;
b) Esboce um gráfico da energia potencial gravitacional e da energia cinética como função da distância percorrida entre e ;
c) Repita o item anterior de forma qualitativa, considerando agora que há uma interação dissipativa entre o ar e o bloco (nesse caso a altura máxima alcançada é menor que ). Inclua também no seu gráfico a energia térmica e energia de fonte do sistema Terra + bloco + ar.
Passo 1
Esse é o típico problema que devemos aplicar as ideias de galileu e newton. Já com relação ao primeiro item, temos a aplicação da equação que relaciona a posição em relação ao tempo
Só que vamos reescrevê-la na direção que realmente iremos usa-la, ou seja, tomando o nosso plano como sendo o , na horizontal e na vertical, teremos que
Passo 2
(a) Nosso primeiro item sugere que um bloco que sobe até a altura e depois cai até atingir o chão, de onde partiu inicialmente.
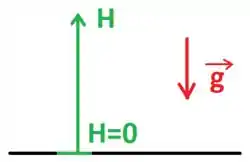
Vamos tomar que nossas condições iniciais são e , assim teremos que
Entretanto vamos supor agora que o bloco subiu até o topo, parou em e vai iniciar sua queda, desta forma temos
Implicando que o tempo de subiu ou descida será de
desta forma teremos que pela primeira equação que encontramos que
Melhorando um pouco a cara desse bixo aí em cima, teremos
E agora mexe aqui .. mexe alí hahaha ... vamos ajeitamos pouco a pouco para chegar em nosso objetivo
Dividimos ambos os lados por
E chegamos em nosso resultado. Mas será que não tem uma forma mais fácil e rápida de chegarmos em nosso resultado? Talvez usando um carinha chamado Torricelli?
Na qual
Talvez de o resultado que queremos...
Tome que quando o bloco chega ao topo, sua velocidade é nula. Então teremos que
Que é o mesmo resultado que chegamos pela relação da equação de posição de função do tempo pra subida e descida.
Passo 3
(b) A energia potencial pode ser descrita por
Enquanto a energia cinética
Plotando nosso gráfico da energia potencial pela distância percorrida pelo bloco, teremos que
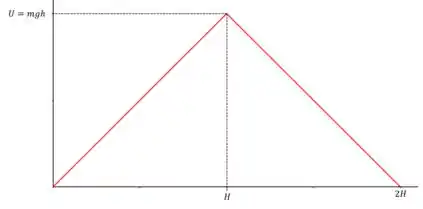
E com relação a energia cinética precisamos determinar a relação da velocidade com a posição. Assim tome do passo que quando o bloco está caindo
Implicando que
E que
Desta forma teremos que
Assim teremos o temos quadrático indica que teremos uma parábola de concavidade para cima. As raízes serão dadas em
Que pode ser resumida em
Então o que temos que em seu ponto mais alto, a energia cinética é nula (já esperávamos por isso né).
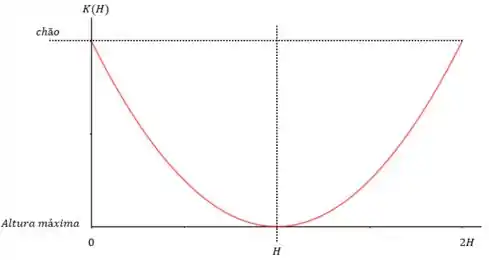
Passo 4
(c) Para a energia potencial, perceba que não teremos uma alteração na cara que o gráfico terá. 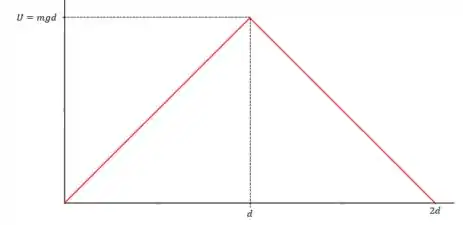
A diferença com relação a primeira hipótese é que agora o bloco não chega a uma altura , mas sim a uma altura , tendo sua energia potencial máxima em .
Com relação a energia cinética, temos que ela até pode ser a mesma no inicio, mas com a resistência do ar, ela se perde por causa da resistência. Resistência essa que leva o nosso bloco a esquentar em certos momentos. Assim temos que a energia térmica se relaciona com a velocidade do bloco.
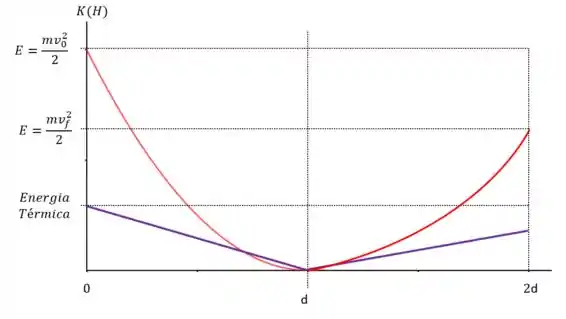
Resposta
- , e
- , e