USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 67e
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
e) Se a partícula tem energia cinética nula quando posicionada em , qual é a energia mínima que deve ser fornecida para que ela possa atingir a posição ? Neste caso, qual sua energia cinética em ?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . A partir disso, temos o gráfico de :
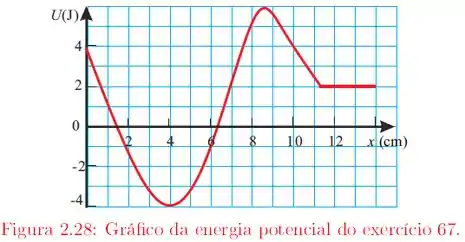
Precisamos analisar o gráfico e determinar o a energia mecânica total, , necessária para que a partícula atinja a posição . E dada essa energia total, determinar o valor da energia cinética em .
Vamos lá!
Passo 2
Observando o gráfico, nós vemos que para a energia potencial é nula, ou seja, . O mesmo acontece em . Repare que existe um poço de potencial nesse intervalo.
Nós precisamos lembrar que a energia sempre se conserva, então no momento em que a energia potencial é mínima, a energia cinética é máxima e vice versa, para que a energia total seja constante. Esse balanço de energia é dado pela equação:
Onde é a energia potencial e a energia cinética. Repare no gráfico que é máxima para . Nesse ponto a energia cinética é mínima, ou seja, . Assim, pela conservação de energia, teremos:
Essa energia total é sempre constante e é o valor mínimo para que a partícula possa atingir a posição .
Passo 3
Olhando novamente para o gráfico, vemos que para , a energia potencial é:
Sendo assim, com , a energia cinética da partícula nesse ponto será:
Valeu, galera! Até a próxima! 😉