USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 67a
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
a) Quais são os pontos ou as regiões de equilíbrio?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . A partir disso, temos o gráfico de :
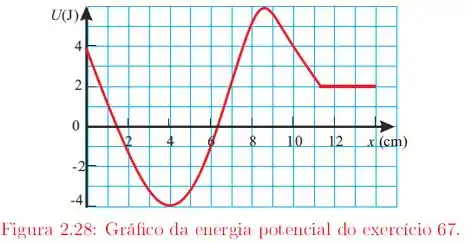
Precisamos determinar os pontos de equilíbrio da função. Para determinar as posições de equilíbrio, precisamos lembrar que elas acontecem quando , ou seja, quando . Além disso, existem três tipos de equilíbrio: o equilíbrio estável (quando o objeto que está em equilíbrio, se move, mas logo em seguida ele volta a posição de equilíbrio), o equilíbrio instável (quando o objeto em equilíbrio, se move e sai do equilíbrio) e o equilíbrio indiferente (quando ele independe das forças e continua sempre em equilíbrio).
Os pontos de equilíbrio acontecem nos pontos críticos da função , onde os pontos de mínimo representam os pontos de equilíbrio estável e os pontos de máximo, seu equilíbrio instável. Vamos analisar cada caso.
Vamos lá!
Passo 2
Apenas observando o gráfico da função , percebemos que existem um ponto de potencial mínimo em e um ponto de máximo em , beleza?
Então, no ponto de mínimo temos um ponto de equilíbrio estável. No ponto de máximo , temos um ponto de equilíbrio instável. Mas repare também que quando vai crescendo de em diantes, a função continua constante. Isso significa que ela está sempre em equilíbrio, independente das forças que estejam atuando, e temos uma região de equilíbrio indiferente para .
Valeu, galera! Até a próxima! 😉