UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 14
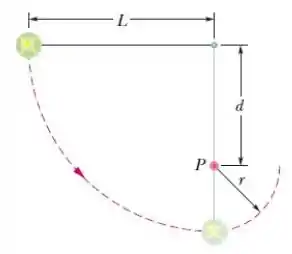
A corda da , e comprimento , possui uma bola presa em uma das extremidades e está fixa na outra extremidade. A distância da extremidade fixa a um pino no ponto é de . A bola, inicialmente em repouso, é liberada com o fio na posição horizontal, como mostra a figura, e percorre a trajetória indicada pelo arco tracejado. Qual é a velocidade da bola ao atingir o ponto mais baixo da trajetória e o ponto mais alto depois que a corda encosta no pino?
Passo 1
Oiie, tudo bem?
Aqui nós temos uma bola presa à uma corda de comprimento . A bola em um altura inicial, é solta e segue a trajetória tracejada indicada na figura
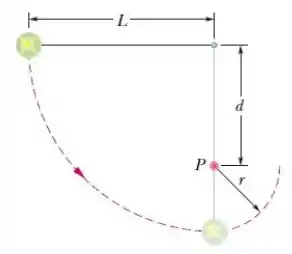
Temos que indica um pino fixo, que está a uma distância da extremidade fixa da corda. Quando a corda colide com o pino, a bolinha passa a seguir uma trajetória que dista do pino, até chegar em uma altura máxima indicada pelo fim do tracejado! O enunciado nos pede para calcular a velocidade quando a bolinha chega no ponto mais baixo, ou seja, logo antes da corda colidir com o pino, e também, a velocidade quando ela chega no ponto mais alto! Mas como fazemos isso?
O caminho mais simples que podemos seguir é utilizar a conservação da energia mecânica para encontrar a velocidade no ponto mais baixo (que escolheremos como referencial de potencial nulo) e depois relacionar esta velocidade ao restante do movimento. Vamos fazer primeiro a alternativa ! Vem comigo!
Passo 2
Como não temos nenhuma força dissipativa atuando sobre o sistema, temos que a energia mecânica se conserva, ou seja, temos que
Isso nos leva a seguinte relação
Então precisamos analisar os valores iniciais da energia potencial e da energia cinética. Inicialmente, temos que a bolinha está a uma altura . Portanto, no referencial que no ponto mais baixo a energia potencial , temos que
Também temos inicialmente que a energia cinética é nula, , já que a bolinha está em repouso, no entanto, ela ganha velocidade até chegar ao ponto mais baixo, e neste instante tem energia cinética dada por
Pela conservação de energia, temos então que
de forma que podemos escrever
A massa pode ser cortada, e se isolarmos a velocidade, temos que
usando que e . Maravilha! Agora só precisamos achar a velocidade dela no ponto mais alto! Consegue visualizar uma maneira de fazer isso? Saca só!
Passo 3
Vamos utilizar a conservação de energia novamente, então temos que
Agora, no entanto, precisamos mudar os valores das energias cinéticas e potenciais, certo? Inicialmente temos a energia cinética dada pela velocidade calculada no passo anterior, ou seja
Mas, não podemos dizer nada sobre a energia cinética final, pois não sabemos se a partícula pára no ponto mais alto da trajetória circular, ou seja temos que
No entanto, sabemos que a energia potencial inicial é nula, , e a energia potencial está relacionada a uma altura relacionada ao topo da trajetória circular que a bolinha realiza após a corda colidir com o pino, como no esquema a seguir
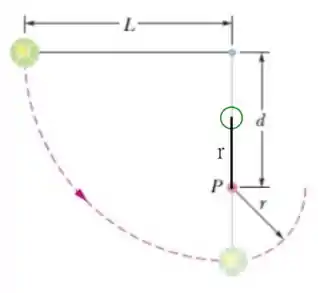
Note que , em que podemos obter o raio fazendo a diferença entre o comprimento da corda e a distância , temos que
resultando em , e portanto, temos que . Ou seja, temos que a energia potencial final é
Belezinha! Agora que relação obtemos da conservação de energia? Veremos no próximo passo!
Passo 4
Temos que
que pode ser simplificada para
Cortando a massa que está em todos os termos, e multiplicando por 2, temos que
se isolarmos a velocidade final que desejamos, temos que
que pode ser calculado para obtermos
A questão foi isso! te vejo na próxima! Tchauzinho!