USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 30c
Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .
Calcule a energia cinética do sistema antes e depois dos patinadores se unirem. Explique o resultado.
Passo 1
Eaew, belezinha?
Temos um sistema que pode ser representado como
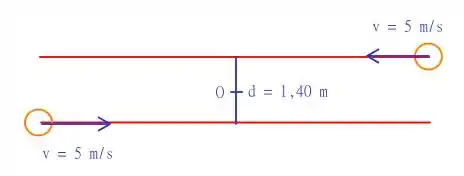
Ambos os patinadores tem e estão se movendo a velocidades , as retas distam de . Precisamos avaliar
Calcule a energia cinética do sistema antes e depois dos patinadores se unirem. Explique o resultado.
Antes dos patinadores darem as mãos temos duas partículas se movendo linearmente, portanto, podemos calcular a energia cinética como
para cada partícula. Após darem as mãos, eles são um sistema de duas partículas vinculadas por uma “barra” de , cujo momento de inércia calculamos na alternativa anterior como
em que . Em que a energia cinética de rotação será agora calculada através de
na alternativa anterior nós obtivemos que
Então, bora lá!
Passo 2
Usando que a massa é e a velocidade dos patinadores antes de dar as mãos é constante igual a , temos que
ou simplesmente
Após darem as mãos, temos agora a energia cinética de rotação como
tal que
Note que a energia cinética do sistema se conserva! Heheheh! A questão foi isso! Te vejo na próxima! Tchau Tchau!