“Minha jangada vai sair pro mar
Vou trabalhar meu bem querer
Se Deus quiser quando eu voltar do mar
Um peixe bom eu vou trazer
Meus companheiros também vão voltar
E a Deus do céu vamos agradecer.”
“Canção da Partida” de Dorival Caymmi.
Esta é a sublime e simples canção de Dorival Caymmi e expressa o desejo que todo pescador tem de ir e voltar da pesca.
Vamos supor que, ao ir para o mar a velocidade da jangada era de (pois estava contra a correnteza) e que sua massa era de e ao voltar, a velocidade da jangada era de (pois está a favor da correnteza) e com uma massa de (pois trouxeram peixes). A variação da energia cinética é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Ele quer que a gente calcule a variação da energia cinética, ou seja:
Passo 2
Do enunciado, temos:
PARA TUDO!!
Olha as unidades!! Tem coisa em e em . Qual que devemos usar??

Acompanha aqui comigo, olhando lá pro enunciado, as alternativas estão em joule que é unidade de energia do SI. Então tudo tem que estar no SI.
E a unidade de velocidade no SI é . Então bora passar a velocidade pra m/s.
Passo 3
Pra gente passar de para é só seguir a tabelinha:
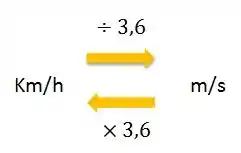
Então:
Show!
Agora é só calcular a variação da energia cinética.
Passo 4
Substituindo esses valores, e calculando:
Maravilha!!!
Resposta
Alternativa D.