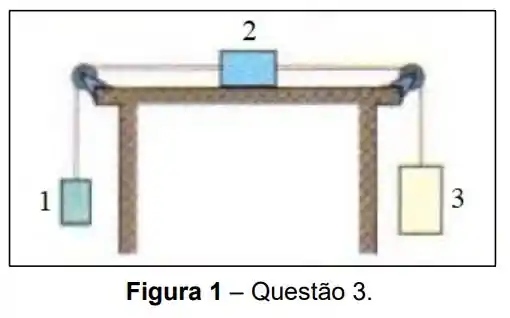
Na figura a seguir temos a imagem de três caixas, ligadas entre si por cordas, de massas desprezíveis, que passam por polias sem atrito. O bloco 2 está sobre uma superfície com coeficiente de atrito cinético de e as massas das caixas são , e . Ao liberarmos as caixas para se movimentarem, qual a tensão na corda da esquerda?
Passo 1
Eaew, tudo certinho com você?
A questão nos traz uma boa imagem que representa o problema
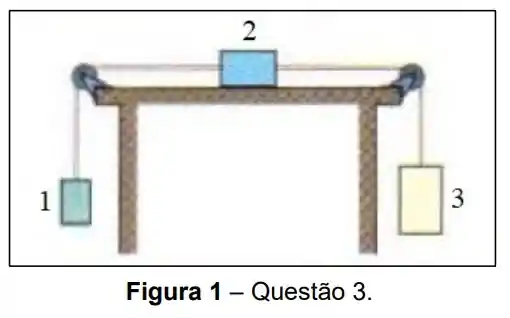
Temos que o bloquinho tem massa , o bloco tem massa e por último o bloco , tem massa . As polias não tem atrito e a corda é inextensível, e ambas de massas desprezíveis. A questão nos pede então para calcular a tensão no bloco da esquerda, ou seja, o bloco . Para resolver esta questão teremos que fazer o balanço das forças que atuam sobre os blocos, e utilizar a segunda lei de Newton para obter um sistema de equações que possibilitará encontrar a tensão desejada! Vamos fazer isso!
Passo 2
O seguinte esquema mostra as forças que atuam sobre esse sistema
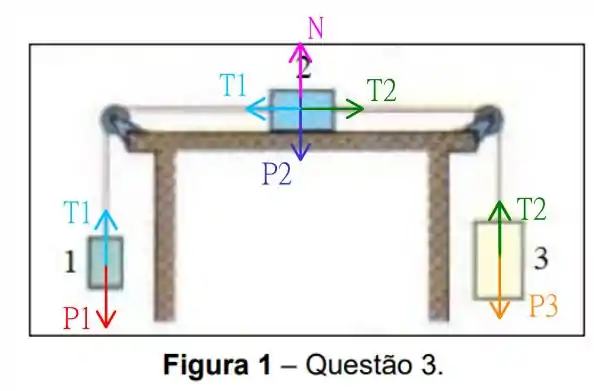
Note que identificar que as tensões no bloco , como as mesmas que na tensão do bloco e , é devido ao fato de termos cordas inextensíveis! Assim podemos escrever três equações relevantes utilizando a segunda lei de Newton, temos que para o bloco 1
A escolha de sinais aqui, indica que estou escolhendo uma aceleração em que o bloco 3 está descendo e o bloco 1 subindo. Para o bloco 2, temos que
e, por último, para o bloco 3, obtemos
Note que para todos os corpos a aceleração é a mesma, pois o sistema se move como um só. Vamos utilizar essas três equações para obter a tensão no bloco 1! Vem comigo!
Passo 3
Se somarmos a equação (2) e a equação (3), temos que
evidenciando a aceleração, e eliminando a tensão no segundo bloco, temos que
Aqui, podemos obter a nossa aceleração em termos de , temos que
Usando esta aceleração vamos poder encontrar a nossa tensão em termos de grandezas conhecidas! Mas vamos ter algum trabalhinho algébrico! Vamos lá!
Passo 4
Se utilizarmos esta aceleração na equação (1), obtemos que
Podemos distribuir os produtos para obter
Se jogarmos o termo de para a esquerda da equação, e o termo de para a direita, temos que
Podemos evidenciar no lado esquerdo e lembrar que e , obtendo
Fazendo MMC do lado esquerdo e do direito, assim como evidenciando do lado direito, temos que
Podemos simplificar os denominadores em ambos os lados, e então evidenciar do lado direito, para finalmente isolar como
Precisamos substituir os valores dados no enunciado, e usando que , obtemos que
A questão é isso! Te vejo na próxima! Tchau Tchau!