USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 67c
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
c) Determine a energia cinética da partícula em ;
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . A partir disso, temos o gráfico de :
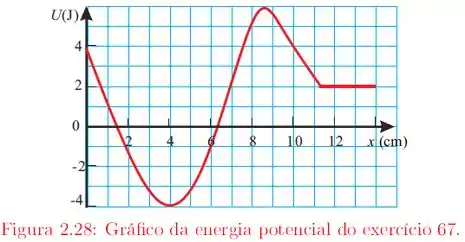
Nós vamos precisar determinar a energia cinética da partícula para . Para isso, vamos usar a informação do item (b), que nos deu a energia mecânica total e as informações do gráfico para fazer o balanço de energia da partícula.
Vamos lá!
Passo 2
Nós sabemos que a energia mecânica tem um valor constante dado por e que ela pode ser escrita conforme a equação:
Ondea energia potencial e a energia cinética são funções da posição da partícula.
Observando o gráfico, nós percebemos que para , a energia potencial da partícula se mantém constante em . Sendo assim, pelo princípio da conservação de energia, temos:
Valeu, galera! Até a próxima! 😉