Uma partícula movendo-se num plano pode ter uma das seguintes velocidades em metros por segundo: (a); (b); (c) ; (d) ; (e) fazendo com o eixo x. Ordene em ordem crescente as energias cinéticas da partícula.
(A)
(B)
(C)
(D)
(E)
Passo 1
Energia cinética é uma grandeza escalar, então, não importa o sentido da velocidade, o que conta é seu módulo (valor).
Assim, basta calcularmos as energias cinéticas para cada uma dessas velocidades.
Lembrando que o módulo de uma velocidade pode ser escrito a partir do teorema de pitágoras para o triângulo retângulo formado pos suas componentes em e :
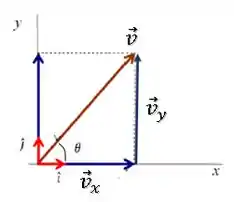
(a)
O módulo de será:
Vamos deixar elevado ao quadrado mesmo, pra já calcular a energia cinética.
(b)
O módulo de será:
Sua energia cinética será:
(c)
O módulo de será:
Sua energia cinética será:
Até agora, temos .
(d)
O módulo de será o valor da própria componente em :
Sua energia cinética será:
(e)
O módulo de para esse caso também já está dado pela questão, podemos ignorar as informações de sua direção:
Sua energia cinética será:
Então ficamos com a seguinte ordem:
Resposta
Letra (A)