USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II, Questão 17b
Considere o espalhamento elástico entre uma partícula alfa de massa por um nêutron em repouso, de massa como mostra a figura.
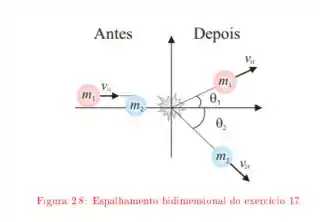
b. Qual é o ângulo entre a direção de recuo e a de incidência?
Passo 1
Eaew, belezinha?
Temos que encontrar o ângulo entre a direção de recuo e a de incidência. Vamos utilizar novamente o triângulo construído no item anterior, aproveitando a conservação do momento linear, e utilizar a lei dos senos.
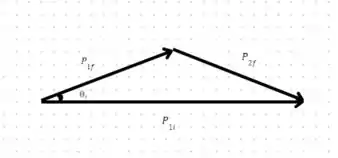
Então vamos lá!
Passo 2
Temos pela lei dos senos que
Temos também pelo item anterior que:
Então, substituindo na lei dos senos
.
Passo 3
A fração da energia cinética incidente que vai para o nêutron é:
.
Temos que a razão entre a energia cinética final total e a inicial é igual a 1, então
Voltando para a relação de e substituindo
.
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
;