Lista de Estudos pra Prova - Stewart Vol 2 - 7°ed de Cálculo Diferencial e Integral 2 da UTFPR - Integrais Duplas

(Cap 15.2 – Ex 21) Calcule a integral dupla.

(Cap 15.2 – Ex 9) Calcule a integral iterada.

(Cap 15.2 – Ex 28) Determine o volume do sólido delimitado pela superfície e pelos planos e .

(Cap 15.2 – Ex 15) Calcule a integral dupla.

(Cap 15.1 – Ex 11) Calcule a integral dupla, identificando-a antes com o volume de um sólido.

(Cap 15.2 – Ex 27) Determine o volume do sólido que está abaixo do paraboloide elíptico e acima do retângulo .

(Cap 15.2 – Ex 17) Calcule a integral dupla.

(Cap 15.2 – Ex 30) Encontre o volume do sólido no primeiro octante limitado pelo cilindro e pelo plano .

(Cap 15.2 – Ex 26) Determine o volume do sólido que se encontra abaixo do paraboloide hiperbólico e acima do retângulo .

(Cap 15.1 – Ex 12) Calcule a integral dupla, identificando-a antes com o volume de um sólido.

(Cap 15.2 – Ex 19) Calcule a integral dupla.

(Cap 15.1 - Ex13) Calcule a integral dupla, identificando-a antes com o volume de um sólido.

(Cap 15.2 – Ex 29) Encontre o volume do sólido delimitado pela superfície e pelos planos e .

(Cap 15.1 – Ex 4) (a) Estime o volume do sólido que está abaixo da superfície e acima do retângulo . Use a soma de Riemann com e escolha os pontos de amostragem como os cantos inferiores esquerdos.

(b) Use a Regra do Ponto Médio para estimar o volume do item (a).

(Cap 15.1 - Ex15) Utilize uma calculadora programável ou computador (ou o comando de soma de um SCA) para estimar

onde . Utilize a Regra do Ponto Médio com os seguintes números de quadrados de tamanhos iguais: e .

(Cap 15.3 – Ex 2) Avalie a integral iterada

(Cap 15.3 – Ex 49) Calcule a integral trocando a ordem de integração.

(Cap 15.3 – Ex 37) Esboce o sólido cujo volume é dado pela integral iterada.

(Cap 15.3 – Ex 13) Expresse D como a região do tipo I e também como uma região do tipo II. Em seguida, calcule a integral dupla de duas maneiras.

D é limitada pelas retas , , .

(Cap 15.2 – Ex 32) Desenhe o sólido que está entre a superfície e o plano e é limitado pelos planos e . A seguir, determine seu volume.

(Cap 15.3 – Ex 31) Determine o volume do sólido dado.

Limitado pelo cilindro e pelos planos , , no primeiro octante.

(Cap 15.3 – Ex 11b) Desenhe um exemplo de uma região que seja

1. Do tipo I, mas não do tipo II
2. Do tipo II, mas não do tipo I

(Cap 15.3 – Ex 21) Calcule a integral dupla.

é limitada pelo círculo de centro na origem e raio

(Cap 15.3 – Ex 25) Determine o volume do sólido dado.

Abaixo da superfície e acima do triângulo com vértices , e

(Cap 15.2 – Ex 31) Encontre o volume do sólido delimitado pelo paraboloide e pelos planos e .

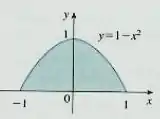
(Cap 15.4 – Ex 2) Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma função qualquer contínua em .

(Cap 15.3 – Ex 20) Calcule a integral dupla.

é limitada por e .

(Cap 15.3 – Ex 14) Expresse D como a região do tipo I e também como uma região do tipo II. Em seguida, calcule a integral dupla de duas maneiras.

D é limitada pelas retas ,

(Cap 15.3 – Ex 22) Calcule a integral dupla.

é a região triangular com vértices e .

(Cap 15.4 – Ex 20) Utilize coordenadas polares para determinar o volume do sólido.

Abaixo do paraboloide e acima do plano .

(Cap 15.4 – Ex 19) Utilize coordenadas polares para determinar o volume do sólido.

Abaixo do cone e acima do disco .

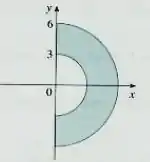
(Cap 15.4 – Ex 4) Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma função qualquer contínua em .

(Capítulo 15.6 – Exercício 1) Determine a área da superfície.

A parte do plano que está acima do retângulo .

(Cap 15.4 – Ex 17) A região dentro do círculo e fora do círculo .

(Cap 15.4 – Ex 9) Calcule a integral dada, colocando-a em coordenadas polares.

Onde R é a região do primeiro quadrante entre os círculos com centro a origem e raios 1 e 3.

(Capítulo 15.4 – Exercício 41) Utilize o resultado do Exercício , parte (c), para calcular as seguintes integrais:

(a)

(b)

(Capítulo 15.4 – Exercício 29) Calcule a integral iterada, convertendo-a antes para coordenadas polares.

(Cap 15.4 – Ex 21) Utilize coordenadas polares para determinar o volume do sólido dado.

Delimitado pelo hiperboloide e pelo plano .

(Capítulo 15.4 – Exercício 32) Calcule a integral iterada, convertendo-a antes para coordenadas polares.

(Cap 15.4 – Ex 22) Utilize coordenadas polares para determinar o volume do sólido dado.

Dentro da esfera e fora do cilindro .

(Cap 15.4 – Ex 27) Utilize coordenadas polares para determinar o volume do sólido dado.

Dentro do cilindro e do elipsoide

(Cap 15.4 – Ex 7) onde é a metade superior do disco com centro na origem e raio 5.

(Cap 15.4 – Ex 8) Calcule a integral dada, colocando-a em coordenadas polares.

Onde R é a região do primeiro quadrante limitada pelo círculo e as retas e .

(Cap 15.4 – Ex 25) Utilize coordenadas polares para determinar o volume do sólido dado.

Acima do cone e abaixo da esfera

(Capítulo 15.4 – Exercício 40)

(a) Definimos a integral imprópria (sobre todo o plano )

onde é o disco com raio e centro na origem. Mostre que

(b) Uma definição equivalente da integral imprópria da parte (a) é

onde é o quadrado com vértices . Use esse resultado para mostrar que

(c) Deduza que

(d) Fazendo a mudança de variável , mostre que

(Esse é um resultado fundamental em probabilidade e estatística.)

(Capítulo 15.5 – Exercício 10) Determine a massa e o centro de massa da lâmina que ocupa a região e tem função densidade .

é delimitada pelas parábolas e ;