James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 2 Problema 31.
(Cap 15.2 – Ex 31) Encontre o volume do sólido delimitado pelo paraboloide e pelos planos e .
Passo 1
Falaiii galerinha, show de bolinhas?
Vamos avaliar o volume da região como uma integral iterada da seguinte maneira
O diagrama de paraboloide , e da seguinte maneira
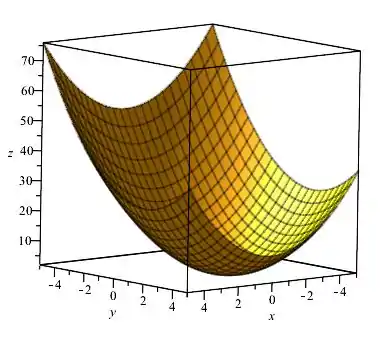
Para que possamos determinar o volume desse sólido, primeiro precisamos escrever uma integral dupla que o descreva. Pra achar os limites de integração, olhamos para os planos que delimilitam o sólido:
Obtemos a partir da equação do paraboloide e da equação do plano , subtraindo-as:
Passo 2
Quando a gente tem uma integral dupla, a gente sempre começa resolvendo de dentro pra fora, assim:
Passo 3
Agora, é só resolver a integral
Beleza?
Resposta
Exercícios de Livros Relacionados
Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.