James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 2 Problema 29.
(Cap 15.2 – Ex 29) Encontre o volume do sólido delimitado pela superfície e pelos planos e .
Passo 1
E ai meus amores, tudo bem?
Bora pra mais uma?
Encostaa!
O enunciado nos dá a seguinte surprefície
E os planos
e .
Acordado com a figura a seguir
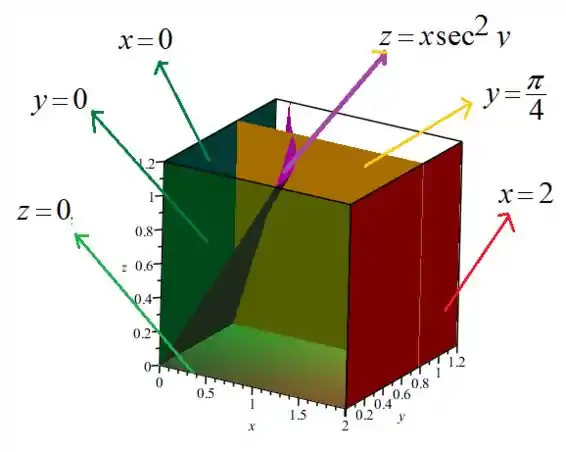
Passo 2
Pessoal, pra determinar o volume desse sólido, primeiro precisamos escrever uma integral dupla que o descreva, que será:
Pra achar os limites de integração, olhamos para os planos que delimilitam o sólido:
Obtemos a partir da equação da superfície:
E agora é só resolver!
Passo 3
Quando temos uma integral dupla, a gente sempre começa resolvendo de dentro pra fora, primeiro com relação a uma das variáveis e depois com relação à de fora:
Passo 4
Agora, é só resolver a integral
Beleza?
Resposta
Exercícios de Livros Relacionados
Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.