(Cap 15.4 – Ex 21) Utilize coordenadas polares para determinar o volume do sólido dado.
Delimitado pelo hiperboloide e pelo plano .
Passo 1
Falaiii gurizadaa, baum por dimais da conta?
Simbora pra mais um?
Dada a expressão do hiperboloide e pelo plano .
Temos que avaliar o volume do sólido contido pelo hiperboloide dado e o plano usando coordenadas polares.
O Hiperboloide de duas folhas hiperboloide intercepta o plano .
Esboçando essa região, temos
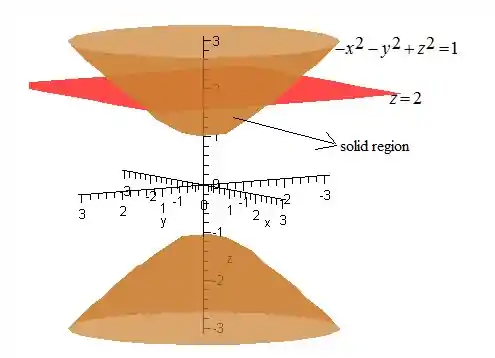
Passo 2
Como a questão pede o volume do sólido delimitado pelo hiperboloide e pelo plano . Vamos achar primeiro a interseção entre eles para assim obtermos o domínio de integração.
Assim, a região de integração será o disco de raio centrado na origem. Além disso, vemos que o plano está acima do hiperboloide nesse domínio, de modo que
Em coordenadas polares:
Passo 3
Fazendo a integral em :
Assim,
Resposta
Portanto, o volume da região sólida necessário é