Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 691234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768707172737475767778798081828384858687888990919293949596979899100

Enunciado

James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 4 Problema 7.

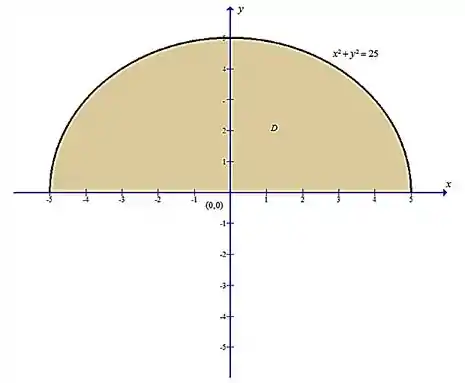
(Cap 15.4 – Ex 7) ∬ D x 2 y   d A ,   onde D é a metade superior do disco com centro na origem e raio 5.

Passo 1

Falaiii gurizadaa, baum por dimais da conta?

Simbora pra mais um?

Cara, a gente quer passar isso pra coordenadas polares, certo?! Belê, vamos lembrar que:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

Se liga, esse J é o nosso Jacobiano, sempre quando a gente faz uma mudança ele é super importante e não podemos esquecer de colocá-lo na integral.

Okay, agora vamos pegar a função ali dentro da integral e ver como ela fica.

∬ D x 2 y   d A = ∬ D [ r cos ⁡ θ ) 2 r sen ⁡ θ   r   d r   d θ = ∬ D r 4 cos 2 ⁡ θ sen ⁡ θ d r   d θ

Passo 2

Manipulando na nossa função, ai beleza, acabou né?! Nããããooooo! Ainda não acabamos. A gente ainda precisa achar os limites de integração

A nossa região D é a parte superior de um disco com centro na origem e raio 5. Mas okay, o que isso pode me dar?! Olha só, vamos começar discutindo sobre o raio.

O disco está centrado na origem e seu raio é 5, ou seja, ele vai da origem até 5, de 0 a 5. Então a variação em r já temos, sendo

0 ≤ r ≤ 5

Show então já sabemos um dos limites de integração!

Agora partindo pra essa questão de ser a parte superior. Quando o disco é completo, ele dá uma volta completa, ou seja, 2 π . Maaas o enunciado nos diz que é só a metade, então ele deu meia volta, ou seja, π . Então, ele saiu de 0 para π , daí

0 ≤ θ ≤ π

Agora que temos nossos limites de integração, vamos resolver nossa integral!!!

Iremos plotar a nossa região D, como mostra a figura a seguir

Passo 3

∫ 0 π ∫ 0 5 r 4 cos 2 ⁡ θ sen ⁡ θ   d r   d θ

Vamos começar fazendo o famoso Fubini e integrando primeiro em relação a d r , ou seja, isso aqui

∫ 0 5 r 4 cos 2 ⁡ θ sen ⁡ θ   d r

Nessa integral, como estamos integrando em relação a d r , podemos tirar cos 2 ⁡ θ s e n θ , porque eles são como constantes nessa integral, então ficamos com:

cos 2 ⁡ θ s e n θ ∫ 0 5 r 4 d r

Agora ficou molezinha, integrando esse r temos isso aqui

cos 2 ⁡ θ sen ⁡ θ   * r 5 5 0 5  

625 cos 2 ⁡ θ sen ⁡ θ  

Agora vamos pegar esse resultado e aplicar na integral de fora!

Passo 4

625 ∫ 0 π cos 2 ⁡ θ sen ⁡ θ d θ

Vamos fazer uma substituição simples

u = cos ⁡ θ

d u = - sen ⁡ θ d θ

625 ∫ - u 2 d u

= - 625 u 3 3

Voltando pra função cos ⁡ θ , teremos:

= - 625 cos 3 ⁡ θ 3 0 π

= - 625 * ( cos 3 ⁡ π - cos 3 ⁡ 0 ) 3

= 1250 3

Resposta

∬ D x 2 y   d A = 1250 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}