James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. - Capítulo 15 - Seção 1 - Problema 11.
(Cap 15.1 – Ex 11) Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Passo 1
Falaaaaii galerinha, show de bolinhas, bora resolver essa comigo?
A integral
Então,
Temos que,
É o volume do sólido que fica acima do retângulo
E abaixo da curva da função
Passo 2
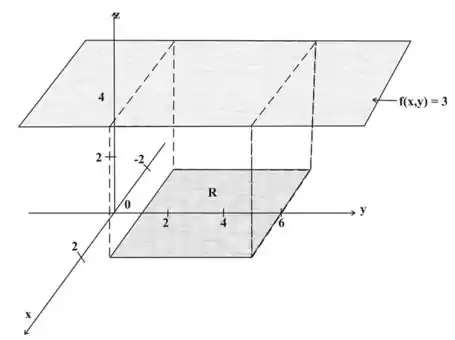
Passo 3
O sólido é um sólido retangular, portanto
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x