James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 3 Problema 37.
(Cap 15.3 – Ex 37) Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
Falaiii gurizadaa, baum por dimais da conta?
Simbora pra mais um?
O problema fornece para gente uma integral iterada e queremos saber qual é o sólido cujo volume é dado por ela.
Vamos lembrar que o volume de um sólido limitado pelo plano e uma superfície dada pela função é a integral dupla dessa função num determinado domínio.
Vamos identificar primeiro o domínio no plano . Observe que varia entre e enquanto varia entre e . Assim, o domínio de integração é representado por
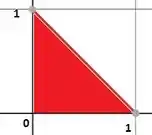
Passo 2
Com isso, o sólido será a região abaixo da superfície sobre a região pintada em vermelho do passo anterior (no plano ). A seguir, represento o domínio de integração em três dimensões:
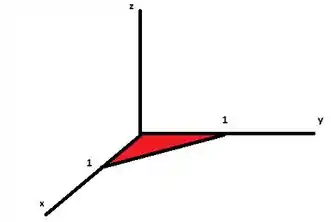
Agora temos que olhar para a superfície . Trata-se de um plano e quando (eixo ), temos . Além disso, quando , temos . Esse plano corta o plano exatamente na reta . Com isso, podemos desenhar o sólido:
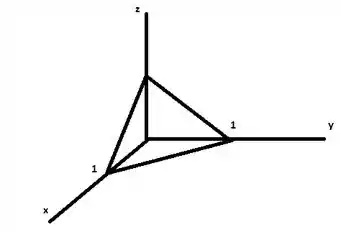
Trata-se de um tetraedro trirretângulo.
Resposta
Esboço de gráfico.