Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 631234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Cálculo - James Stewart - Volume 2 - 7ª Edição – Capítulo 15 – Seção 4 – Exercício 32

(Capítulo 15.4 – Exercício 32) Calcule a integral iterada, convertendo-a antes para coordenadas polares.

∫ 0 2 ∫ 0 2 x - x 2 x 2 + y 2   d y   d x

Passo 1

Faaaala meus queridos

Se liga só, nesse exercício temos uma integral duplinha:

∫ 0 2 ∫ 0 2 x - x 2 x 2 + y 2   d y   d x

E aí vamos calcular essa integral usando a conversão pra coordenadas polares, feshow?

Lembrando que nas coordenadas polares, vamos fazer

x = r . cos ⁡ θ

y = r . s e n   θ

E o Jacobiano dessa transformação é J = r

Então boraaa

Passo 2

Temos a integral

∫ 0 2 ∫ 0 2 x - x 2 x 2 + y 2   d y   d x

Fazendo a substituição para coordenadas polares, vamos ter: x = r . cos ⁡ θ

y = r . s e n   θ

E portanto

x 2 + y 2 = r . cos ⁡ θ 2 + r . s e n   θ 2 = r 2 . c o s 2 θ + s e n 2 θ = r 2 . 1 = r ²

Vamos reparar também que, pelos intervalos de integração, 0 ≤ y ≤ 2 x - x 2 , então vamos fazer algumas contas com isso:

y ≤ 2 x - x 2

r   s e n   θ ≤ 2 r cos ⁡ θ - r 2 cos 2 ⁡ θ

r 2 s e n 2 θ ≤ 2 r cos ⁡ θ - r 2 cos 2 ⁡ θ

r 2 ≤ 2 r cos ⁡ θ

r ≤ 2 cos ⁡ θ

Então devemos ter 0 ≤ r ≤ 2 cos ⁡ θ . Agora, vamos fazer um esboço da região pra sabermos os limites em θ :

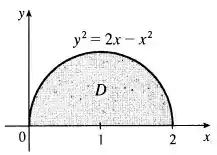
Veja que a região está restrita ao primeiro quadrante, então devemos ter 0 ≤ θ ≤ π 2 . Agora é só escrever a integral em coordenadas polares:

∫ 0 π / 2 ∫ 0 2 cos ⁡ θ r 2   r   d r   d θ

Passo 3

Show! Agora lembre-se de que, pra calcular a integral dupla, sempre começamos de dentro pra fora:

∫ 0 π 2 ∫ 0 2 cos ⁡ θ r 2   r   d r   d θ

Calculando a integral de dentro:

∫ 0 π 2 ∫ 0 2 cos ⁡ θ r 2 d r d θ

∫ 0 π 2 r 3 3 0 2 cos ⁡ θ d θ

Showw, agora nos resta a integral de fora:

∫ 0 π 2 8 3 cos 3 ⁡ θ d θ

8 3 s e n   θ - s e n 3 θ 3 0 π 2

8 3 1 - 1 3

Então:

∫ 0 π 2 ∫ 0 2 cos ⁡ θ r 2   r   d r   d θ = 16 9

Resposta

16 9

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}