Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes por Integrais Duplas

Ver Teoria
Exercício 521234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515354555657585960616263646566676869707172737475767778798081828384858687888990

Enunciado

James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 4 Problema 25.

(Cap 15.4 – Ex 25) Utilize coordenadas polares para determinar o volume do sólido dado.

Acima do cone z = x 2 + y 2 e abaixo da esfera x 2 + y 2 + z 2 = 1

Passo 1

Beleza, galera?

Vamos pra mais uma?

O objetivo é usar coordenadas polares para encontrar o volume do sólido dado.

A figura a seguir mostra o sólido dado

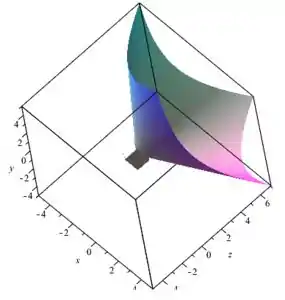
Passo 2

A equação da esfera x 2 + y 2 + z 2 = 1 pode ser reescrita como

z 2 = 1 - ( x 2 + y 2 )

x = r c o s   θ ,   y = r s i n   θ

O hemisfério superior limitado abaixo pelo plano xy, é

z = 1 - ( x 2 + y 2 )

= 1 - r 2

A expressão do cone é

z = x 2 + y 2

= r 2  

= r

Ao olharmos para o volume abaixo da esfera e acima do cone , z = 1 - r 2 - r

Passo 3

Definindo a equação da esfera e do cono iguais, então a interseção para ser um círculo como

x 2 + y 2 + x 2 + y 2 2 = 1

x 2 + y 2 + x 2 + y 2 = 1

2 x 2 + y 2 = 1

x 2 + y 2 = 1 2

r 2 = 1 2

r = 1 2

r = 2 2

Com base nas informações obtidas com os cálculos realizados, a região de integração é o circuilo de raio 2 / 2 centrado na origem, que imediatamente pode ser escrita em coordenadas polares como

D = r ,   θ 0 ≤ r ≤ 2 2 ,   0 ≤ θ ≤ 2 π

Passo 4

O volume do sólido é

V = ∬ R z d x d y

= ∫ 0 2 π ∫ 0 2 2 1 - r 2 - r r d r d θ

= ∫ 0 2 π ∫ 0 2 2 ( r 1 - r 2 - r 2 ) d r d θ

= ∫ 0 2 π ∫ 0 2 2 1 2 × 2 r 1 - r 2 - r 2 d r d θ

= ∫ 0 2 π - 1 2 × 1 - r 2 3 2 3 2 - 1 3 r 3 0 2 2 d θ  

= ∫ 0 2 π 1 6 2 - 2 d θ

= 1 6 2 -   2 θ 0 2 π

= 1 6 2 - 2 ( 2 π )

= π 3 2 - 2    

Resposta

Portanto, o volume nexessário do sólido é

π 3 2 - 2    

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.