(Cap 15.1 - Ex13) Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Passo 1
E aiii, cêis tão bonzinho?
Espero que sim.
Vamos resolver essa comigo?
Simboráa
Considerando a seguinte integral
O objetivo é analisar a integral dupla identificando – a primeiro como um volume de um sólido.
Desde ,
Portanto, a integral dada representa o volume dessa parte do sólido retangular que se encontra abaixo do plano
Passo 2
Esbocando a figura a seguir, temos
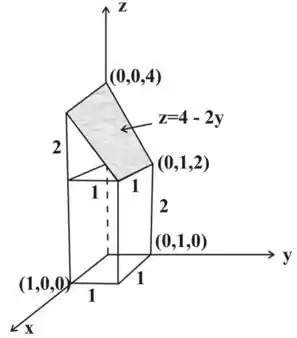
Passo 3
O volume de um prisma trapezoidal é da seguinte maneira:
Fórmulas:
O volume do cubo é :
O volume de um prisma reto é :
Considerando
Temos que
Resposta
Portanto, o volume de um sólido é .