Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 3 Problema 49.
(Cap 15.3 – Ex 49) Calcule a integral trocando a ordem de integração.
Passo 1
Falaiiii seres de luz, tudo na paz?
Bora resolver mais uma?
Encostaaaaa
O primeiro passo é esboçar a região:
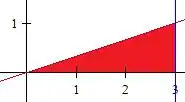
Invertendo a ordem de integração, temos que vai de até , enquanto vai do eixo () até a reta . Assim,
Passo 2
Fazendo a primeira integral em :
Assim, chamando , temos que . Assim,
Resposta
Portanto, o valor integral é
Exercícios de Livros Relacionados
Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos x1 + cos 2 xd xd y
Inverta a ordem de integração.