(Cap 15.3 – Ex 14) Expresse D como a região do tipo I e também como uma região do tipo II. Em seguida, calcule a integral dupla de duas maneiras.
D é limitada pelas retas ,
Passo 1
Falaiii galerinha, show de bolinhas?
Sabemos que ...
Temos um problema de integração em uma região geral. Precisamos entender que tipo de região estamos trabalhando para poder resolver a integral.
Uma região do tipo 1 é uma região limitada acima e abaixo por uma curva, além disto, é limitada lateralmente por retas verticais. Portanto, o seu domínio é:
Já uma região do tipo 2 é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais. Portanto, temos o seguinte domínio:
Vamos começar por esboçar o gráfico da nossa região. Posteriormente, vamos escrever cada uma das regiões.
Passo 2
Primeiramente, vamos esboçar a nossa região. Portanto,
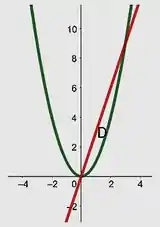
As duas curvas se intersectam nos pontos em que:
e
Portanto, no ponto e no ponto .
Passo 3
Agora podemos começar a escrever a nossa região. Como a região do tipo I é limitada pelas curvas em cima e embaixo, então é a variável que vai ser limitada por essas curvas:
Já os limites laterais são definidos pelos pontos calculados no passo 2:
Portanto, a nossa integral é:
Resolvendo-a, temos:
Passo 4
Vamos escrever a nossa região como uma região do tipo II. Ela é limitada a esquerda por uma curva e a direita por outra curva. Portanto, agora vai ser a variável que será limitada pelas curvas:
Acima ela é limitada pela reta (se resume a um ponto) e abaixo por outra reta . Observem que estas retas são dadas pelos pontos de interseção das curvas. Portanto, a nossa integral é:
Resolvendo-a, temos:
Resposta
Portanto, a integral do tipo I é