James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. - Capítulo 15 - Seção 1 - Problema 15.
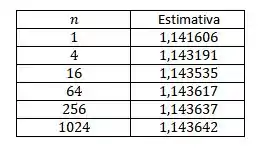
(Cap 15.1 - Ex15) Utilize uma calculadora programável ou computador (ou o comando de soma de um SCA) para estimar
onde . Utilize a Regra do Ponto Médio com os seguintes números de quadrados de tamanhos iguais: e .
Passo 1
Falai pessoal do responde ai, tudo certinho?
Bora para mais uma ?
Simborá então
Considerando a integral
Com região .
Usando CAS (maple) para calcular a integral para 1, 4, 16, 64, 256 números iguais de quadrados.
A Regra do Ponto Médio afirma que o volume sob uma superfície sobre uma região R pode ser aproximado por
A área do quadrado menor com comprimento é :
Passo 2
Resposta
Exercícios de Livros Relacionados
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}