James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 3 Problema 21.
(Cap 15.3 – Ex 21) Calcule a integral dupla.
é limitada pelo círculo de centro na origem e raio
Passo 1
Alô Alô, bora lá galerinha..
Vemmm comigoo!!
Considerando a seguinte integral
Onde D é limitado pelo círculo com centro na origem e raio é.
O objetivo é avaliar a integral dupla
Com base na imagem a seguir, temos
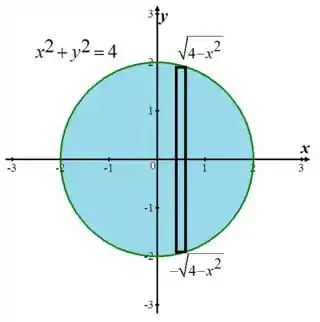
Para analisarmos a região , a queação do círculo dito no enunciado é
Podemos isolar uma das variáveis, vamos isolar
Podemos dizer então que , enquanto varia entre e onde é o raio, como , .
Passo 2
Então temos que
Agora é só integrar, primeiro em relação a
Passo 3
Agora em relação a , vamos fazer a substituição e esquecer os limites de integração por enquanto
Então a integral é
Substituindo de volta
Então temos que
Resposta
Portanto, a integral avaliada é
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x