James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 4 Problema 27.
(Cap 15.4 – Ex 27) Utilize coordenadas polares para determinar o volume do sólido dado.
Dentro do cilindro e do elipsoide
Passo 1
Falaiii galerinha, show de bolinhas?
Sabemos que ...
Para calcular o volume do sólido, vamos primeiramente construir uma integral dupla que o represente. Depois vamos calcular a integral.
A figura a seguir mostra o sólido dentro do cilindro e do elipsoide
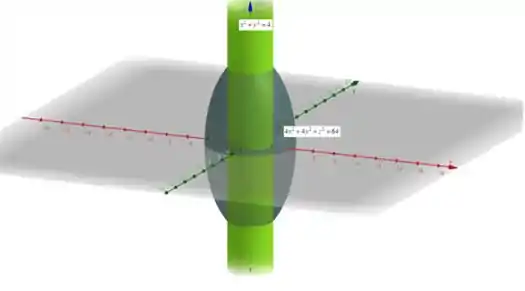
Passo 2
Vamos começar achando os limites de integração!
Como o sólido está dentro cilindro , ele que vai limitar a região de integração. Passando para coordenadas polares, teríamos
Substituindo na equação, temos que a região de integração está limitada no seguinte intervalo,
Passando para o elipsoide, vamos aplicar as coordenadas polares e isolar
Agora podemos montar a nossa integral, não esquecendo de multiplicar pelo nosso Jacobiano . Então, o volume da metade superior do sólido é calculado pela integral:
Pra calcular o volume do sólido inteiro, é só multiplicar a integral por :
Passo 3
Podemos separar a integral no produto de duas integrais simples:
Show?