James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. - Capítulo 15 - Seção 1 - Problema 12.
(Cap 15.1 – Ex 12) Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Passo 1
Falaiii meus amigos, show de bola?
Bora pra mais um?
Simboráa
Precisamos calcular uma integral dupla, numa dadaregião de integração!
A integral é
A região de integração é
O objetivo será avaliar a integral dupla identificando-a como volume de sólido
Primeiro de tudo, iremos esboçar o diagrama da região , da seguinte maneira:
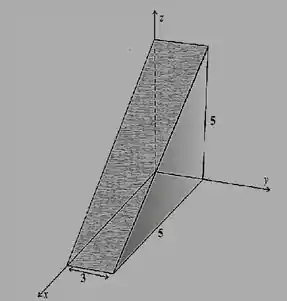
Passo 2
Interpretaremos como a hipotenusa de um triângulo retângulo no plano , de , sendo esse um triângulo retângulo isósceles com os dois catetos iguais a 5. Em , a região ocupa o intervalo , e nós interpretaremos isso como a altura do objeto sólido que é igual a 3.
Interpretando essa integral como volume de um prisma retangular reto, temos:
onde serão as pernas do prisma triangular direito.
Resposta
Portanto, a integral dupla é igual a .