(Cap 15.3 – Ex 31) Determine o volume do sólido dado.
Limitado pelo cilindro e pelos planos , , no primeiro octante.
Passo 1
Falaiiii seres de luz, tudo na paz?
Bora resolver mais uma?
Encostaaaaa
O domínio de integração está no plano (ou ) e a “tampa” do sólido é dada pelo plano . Assim, devemos integrar a função no domínio de integração limitado pela circunferência no plano :
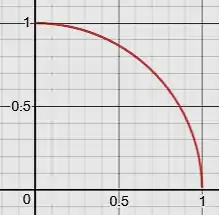
Assim, o volume será
Passo 2
Calculando a primeira integral:
Assim,
Resposta
Portanto, o volume do sólido é: